Основание пирамиды - прямоугольный треугольник с катетами 15 и 20 см. Высота пирамиды равна 16см и проходит через вершину прямого угла. Найдите площадь сечения пирамиды, проходящего через ее высоту перпендикулярно к гипотенузе основания.
Ответы
1)Построим данное сечение:строим АМ перпендикуляр к гипотенузе ВС, тогда ДМ перпендикуляр к ВС (теорема о 3-х перпендикулярах).ДМ -наклонная, ДА-перпендикуляр к пл-ти АВС, АМ-проекция наклонной, тогда ВС перпендикулярна и к ДМ, след-но ВС пер-на плоскости(АДМ).
2) Площади тр-ка АДМ-прям. равна S= 0,5*АД* АМ. ! АД=16 см , АМ-?
3) Из тр-ка АВС-прям.:
ВС=25 см, т.к. данный тр-к подобен " египетскому" (!!! 3,4,5) с коэфф.5.
Площадь АВС равна: S1= 0,5*АВ*АС=0,5*20*15=150 (см^2).
С др. стороны S1= 0,5*ВС*АМ=150
0,5* 25*АМ =150
АМ =12.
4)S = 0,5*АД* АМ= = 0,5*16* 12= 96 (cм^2).
Ответ: 96 cм^2.
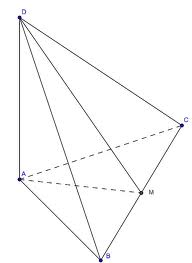
В сечении получается прямоугольный треугольник с катетом 16 (это высота пиармиды), а второй катет - это высота прямоугольного треугольника в основании пирамиды, проведенная к гипотенузе (раз мы сечем плоскостью перпендикулярной гипотенузе, то и линяя пересечения плоскостей перпендикулярна ей, то есть это - высота треугольника).
Треугольник с катетами 15 и 20, поэтому гипотенуза 25 (подобен египетскому 3,4,5).
Высоту его можно сосчитать кучей сопособов, проше всего так
h*25 = 15*20; h = 12;
Итак, в сечении прямоугольный треугольник с катетами 12 и 16 (опять 3,4,5:), его площадь 12*16/2 = 96;
