14.5. Найдите разность арифметической прогрессии (а), если:
1) a, = 18, n = 27, S, = 2241;
2) a, = -8, n = 17, S, = -408;
3) a, = -5, n = 23, S, = 1909;
4) a, = 81, n = 34, S, = 510.
СРОЧНОО (˚ ˃̣̣̥⌓˂̣̣̥ ) !!
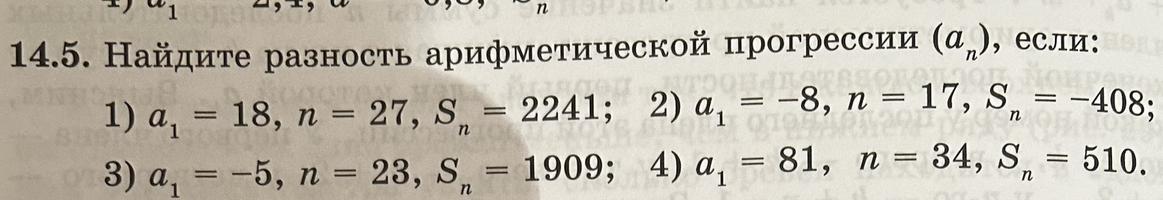
Ответы
Відповідь:
Чтобы найти разность арифметической прогрессии (d), используем формулу для суммы арифметической прогрессии:
S = (n/2)(2a + (n - 1)d),
где S - сумма, n - количество членов прогрессии, a - первый член, d - разность.
1) Для S1 = 2241, a1 = 18, n1 = 27:
2241 = (27/2)(2*18 + (27 - 1)*d1),
4482 = 810 + 26d1,
3672 = 26d1,
d1 = 3672/26,
d1 = 141.23.
2) Для S2 = -408, a2 = -8, n2 = 17:
-408 = (17/2)(2*(-8) + (17 - 1)*d2),
-816 = -272 + 16d2,
-544 = 16d2,
d2 = -544/16,
d2 = -34.
3) Для S3 = 1909, a3 = -5, n3 = 23:
1909 = (23/2)(2*(-5) + (23 - 1)*d3),
3818 = -230 + 22d3,
4048 = 22d3,
d3 = 4048/22,
d3 = 184.
4) Для S4 = 510, a4 = 81, n4 = 34:
510 = (34/2)(2*81 + (34 - 1)*d4),
1020 = 540 + 33d4,
480 = 33d4,
d4 = 480/33,
d4 = 14.54.
Таким образом, разности для каждой последовательности равны:
1) d1 = 141.23,
2) d2 = -34,
3) d3 = 184,
4) d4 = 14.54.
якщо можна дай кращу відповідь