Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Обчисліть інтеграли.
Приложения:
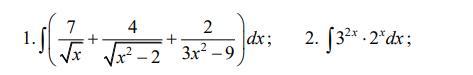
Ответы
Автор ответа:
1
Ответ:
Найти неопределённый интеграл . Применяем формулы 3 , 12 , 13 и 5 .
Приложения:
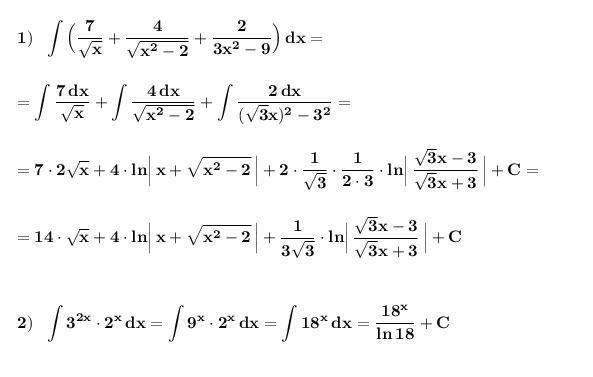

fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: Физика,
автор: sofikud
Предмет: Қазақ тiлi,
автор: jutle956
Предмет: Қазақ тiлi,
автор: mailk9139
Предмет: Литература,
автор: Аноним
Предмет: Другие предметы,
автор: 1234567891aruzhan