Question

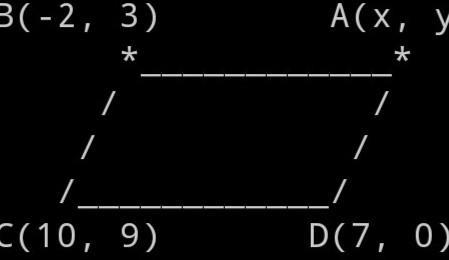
Чотирикутник ABCD - паралелограм. Задано три його вершини: B (-2; 3), C (10; 9), D (7; 0). Знайдіть координати вершини А. Обов‘язково зробити з малюнком!Поставлю як найкращу відповідь

Answer 1

Объяснение:

Щоб знайти координати вершини A паралелограма ABCD, можемо скористатися тим, що протилежні сторони паралелограма рівні за довжиною і паралельні. Таким чином, вектор CD повинен бути рівний вектору BA.

1. Знайдіть вектор CD, віднявши координати точки C від координат точки D.

2. Застосуйте цей вектор до точки B, щоб знайти координати точки A.

Зображення:

Розрахунок:

1. Вектор CD = (7 - 10, 0 - 9) = (-3, -9).

2. Координати точки A = B + CD = (-2, 3) + (-3, -9) = (-5, -6).

Отже, координати вершини A паралелограма ABCD дорівнюють (-5, -6).