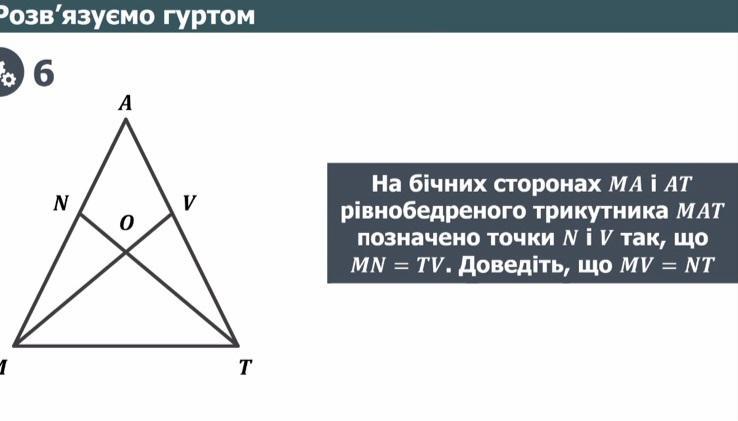
Буль ласка допоможіть завдання на фото
Ответы
Ответ:
Розглянемо рівнобедрений трикутник MAT, де MA = MT.
Оскільки MN = TV та MA = MT, то, згідно із властивостями рівнобедреного трикутника, можемо сказати, що трикутники MAN і TAV є рівними за сторонами-сторонами-сторонами (SSS).
Отже, вони мають відповідні рівні сторони та відповідні рівні кути.
У трикутнику MAN рівні сторони MA та MN відповідають сторонам TA та TV у трикутнику TAV.
Оскільки кути напротиж однакових сторін у рівнобедреному трикутнику рівні, то можемо сказати, що кут MAN = кут TAV і кут MAT = кут TAT.
Розглянемо тепер чотирикутник MVAN. У цьому чотирикутнику сума всіх кутів дорівнює 360 градусів.
Кут MVN + кут VAN + кут ANM + кут MVT = 360 градусів.
Оскільки кут ANM = кут TAV і кут MVT = кут TAT (оскільки AM = AT, і MAT = TAT), то можемо замінити ці значення:
Кут MVN + кут VAN + кут TAV + кут TAT = 360 градусів.
Але кут MVN = кут VAN (оскільки MA = MA), отже, можемо замінити це значення:
2 * кут VAN + кут TAV + кут TAT = 360 градусів.
Кут TAV + кут TAT = 180 градусів, оскільки трикутник TAT є прямокутним.
Отже, отримали, що:
2 * кут VAN + 180 градусів = 360 градусів.
2 * кут VAN = 180 градусів.
Кут VAN = 90 градусів.
Тепер розглянемо трикутники MVN і TAV. Вони є прямокутними трикутниками з кутом VAN = 90 градусів.
Отже, MV та NT є відомими нам сторонами, які лежать проти прямого кута в обох трикутниках.
За теоремою Піфагора у прямокутному трикутнику відомо, що квадрат гіпотенузи (у нашому випадку MV або NT) дорівнює сумі квадратів катетів (у нашому випадку MN і VN або TV і TM).
Таким чином, \(MV^2 = MN^2 + VN^2\) та \(NT^2 = TV^2 + TM^2\).
Оскільки MN = TV, то \(MV^2 = VN^2\) і \(NT^2 = TM^2\).
Отже, \(MV = VN\) та \(NT = TM\).
Отже, доведено, що \(MV = NT\).