Question

Плииз!! Вычислить площадь параллелограмма, построенного на векторах a и b.

a=2p+3q, b=p-2q
вектор p = 2,
вектор q=3
(p,q)=п/4

14 задание на фото!!!

Answer 1

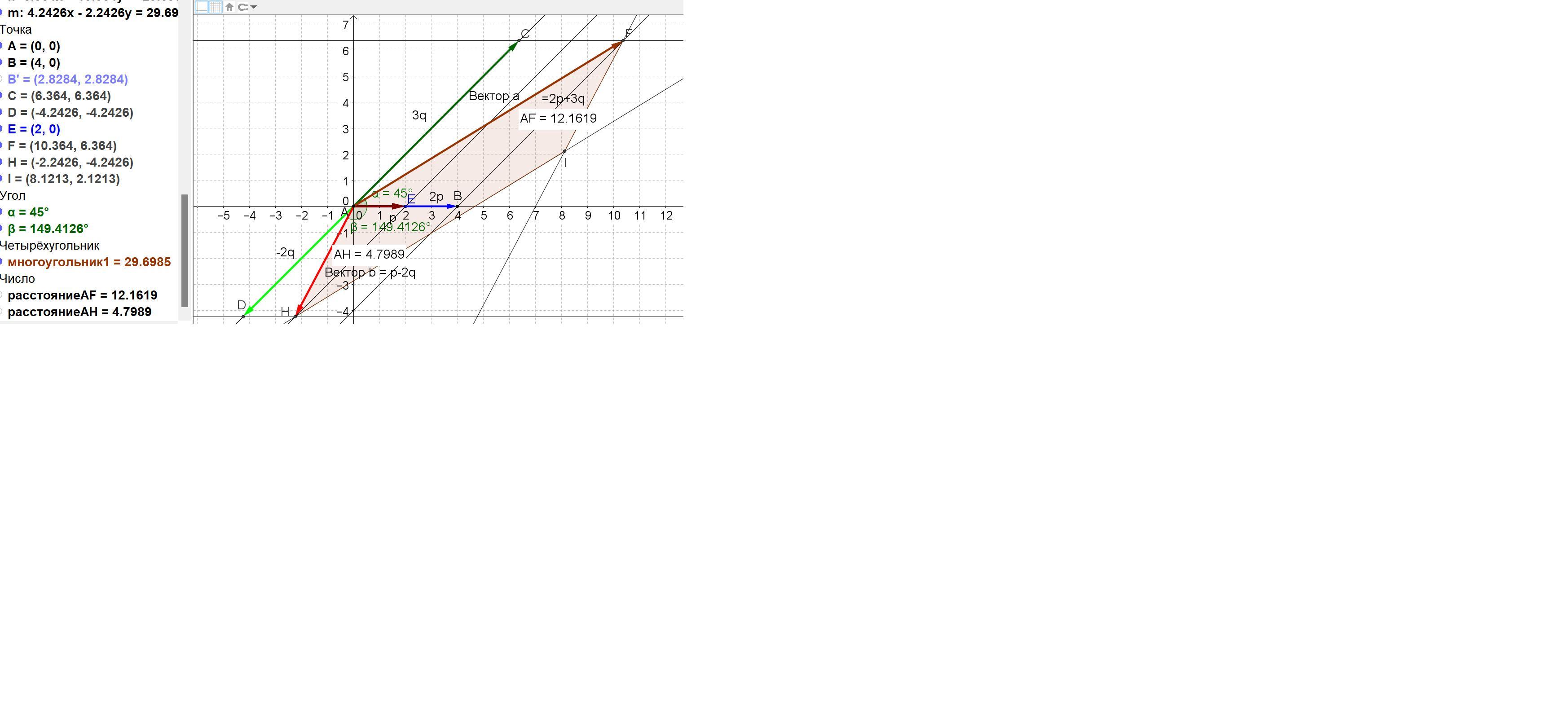
Ответ: S =  29,69848481 кв. ед.

Пошаговое объяснение:

Находим модули векторов а и b и их произведение.

(2p+3q)(p-2q) =  2 p^2 + 3 pq + -4 pq -6 q^2

= 8  + -8,485281374  +   -54 =

= -50,24264069.

Модуль а = √((2p+3q)^2) = √(4p² + 12pq*cos45 + 9q²) = √(16 + 72*(√2/2) + 81) =

               = √(97 + 36√2).

Модуль b = √((p-2q)^2) = √(p² - 4pq*cos45 + 4q²) = √(4 – 24*(√2/2) + 36) =

               = √(40 - 12√2).

cos(a_b) = -50,24264069/(√(97 + 36√2)* √(40 - 12√2)) = -0,86085409.

Находим синус угла: sin(a_b) = √(1 - cos²( a_b)) = 0,508851879.

Теперь можно найти площадь параллелограмма как произведение модулей векторов a и b и на синус угла между ними.

S = a*b*sin(a_b) = √(97 + 36√2)* √(40 - 12√2)* 0,508851879 =

= 29,69848481 кв. ед.