Предмет: Алгебра,
автор: denpotop823
СРОЧНО ПОМОГИТЕ !!!!
ДАЮ 40 балов
Приложения:
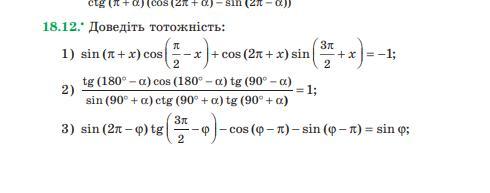
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: kseniarasevs1317
Предмет: Английский язык,
автор: diniskoviktoria837
Предмет: Химия,
автор: kirilyk2007
Предмет: Русский язык,
автор: kirakkkamys
Предмет: Алгебра,
автор: dsuperkotik