Предмет: Алгебра,
автор: masha01021
Помогите пожалуйста решить задачу 12 , общее решение
Приложения:
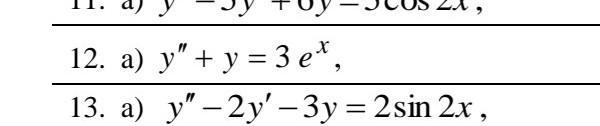
yugolovin:
y=C_1 cos x+C_2 sin x+(3/2) e^x
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Если такой простой способ вызывает сомнения, можно работать по стандартной схеме.
Сначала решаем однородное уравнение
с помощью характеристического уравнения:
Далее ищем частное решение неоднородного уравнения в виде
подставляя в уравнение, получаем
а тогда общее решение уравнения имеет вид
спасибо большое
вы лучший
если время будет то решите пожалуйста и другой вопрос
вы здесь?
Похожие вопросы
Предмет: Математика,
автор: demrok2012
Предмет: География,
автор: klintsovay
Предмет: Оʻzbek tili,
автор: muhammadumarh777
Предмет: Математика,
автор: 20111702140389
Предмет: Математика,
автор: madina388887