Question

Висота циліндра дорівнює 10 см, а
діагональ його осьового перерізу утворює
з площиною основи кут 60°. Знайти площу
осьового перерізу циліндра.

Answer 1

Ответ:

Площа осьового перерізу циліндра становить $\bf \dfrac{100\sqrt{3} }{3}$ см².

Объяснение:

Висота циліндра дорівнює 10 см, а діагональ його осьового перерізу утворює з площиною основи кут 60°. Знайти площу осьового перерізу циліндра.

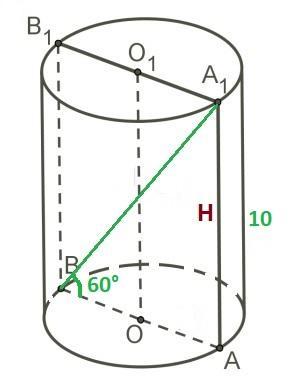
Осьовим перерізом циліндра є прямокутник AA₁B₁B, сторони AA₁=BB₁ якого є твірними циліндра (їх довжина дорівнює висоті H циліндра), а інші дві сторони AB=A₁B₁ – діаметри основ циліндра.

Отже AA₁ = Н = 10 см.

Оскільки осьовий переріз перпендикулярний до площини основи циліндра (звідси АА₁⊥AB), проходить через його вісь ОО₁ (за означенням), то ∠А₁ВА – кут між діагоналлю A₁B перерізу і площиною основи циліндра (діаметр основи AB є ортогональною проекцією діагоналі A₁B осьового перерізу AА₁B₁B).

Отже, ∠А₁ВА = 60°

Розглянемо прямокутний трикутник ABА₁ (∠A₁АB=90°), у якого AB - прилеглий катет, а АА₁ - протилежний катет до ∠А₁ВА = 60°.

За означенням тангенса гострого кута прямокутного трикутника маємо:

$tg \angle A_1DA=\dfrac{AA_1}{AB}$

$AB = \dfrac{AA_1}{tg 60^\circ} =\dfrac{10}{\sqrt{3} } =\bf \dfrac{10\sqrt{3} }{3}$ (см)

Площа прямокутника AA₁B₁B (осьового перерізу):

Sпер = AA₁ · AB

  $S = 10 \cdot\dfrac{10\sqrt{3} }{3} = \bf\dfrac{100\sqrt{3} }{3}$ (см²)

#SPJ1