Предмет: Алгебра,
автор: bektur2244
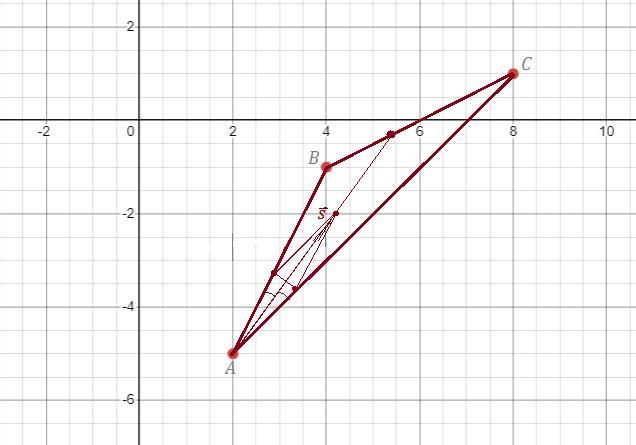
Даны точки А (2; -5), В (8; 1) и с (4; -1) - вершины треугольника АВС. Найти: - а) уравнение биссектрисы AP
Приложения:

Ответы
Автор ответа:
1
Ответ:
Уравнение биссектрисы АР .
Найдём координаты векторов АВ и АС .
Теперь найдём координаты единичных векторов , лежащих на векторах АВ и АС .
Если построить на единичных векторах параллелограмм , то он будет ромбом, так длины его сторон равны длинам единичных векторов , а они равны 1 . Значит диагональ ромба, равная сумме единичных векторов , будет направлена по биссектрисе ( диагонали ромба являются биссектрисами его углов ) . Найдём направляющий вектор биссектрисы .
Можно взять вектор, коллинеарный сумме единичных векторов :
Запишем уравнение биссектрисы AP , проходящей через точку А , параллельно вектору s :
Можно теперь записать уравнение биссектрисы через нормальный вектор (а можно и не писать) :
Приложения:
Похожие вопросы
Предмет: История,
автор: esapovalow
Предмет: Другие предметы,
автор: faz596da7
Предмет: География,
автор: sergeyosa130910
Предмет: Геометрия,
автор: vladislavan89