Question

5. Найдите площадь криволинейной трапеции, ограниченной линиями:
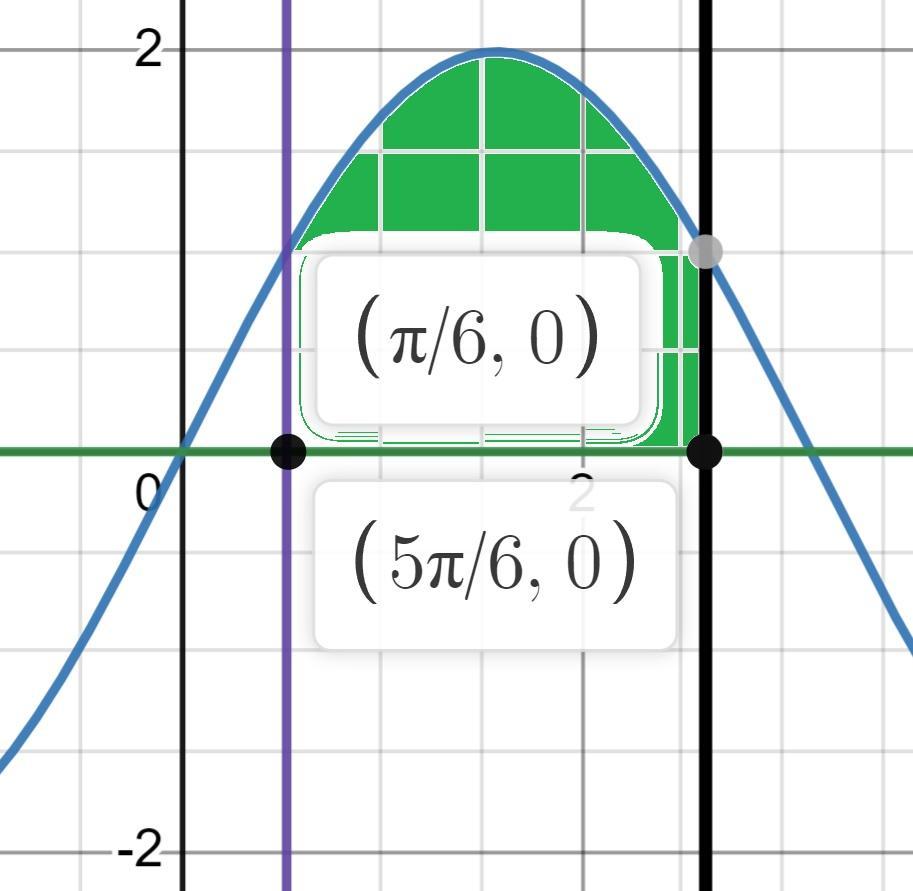
y = 2 sin x, y = 0, х1 =п/6, х2=5п/6

Answer 1

Ответ:  2√3 кв.ед.

Объяснение:

Строим  графики функций y = 2 sin x, y = 0, х1 =п/6, х2=5п/6.(См. скриншот)

Площадь S=∫(a;b) (f₁(x)dx - f₂(x)dx);

Пределы интегрирования  a=π/6;  b=5π/6.

f₁(x) = 2sinx;

f₂(x) = 0.  Тогда

S=∫(π/6; 5π/6)(2sinx-0)dx = ∫(π/6; 5π/6)(2sinx) = -2 cosx|(π/6; 5π/6) =

= -2(cos5π/6 - cosπ/6) = -2(-√3/2 - √3/2) = -(-2√3) = 2√3 кв.ед.