Предмет: Алгебра,
автор: bogdanaromenko006
Допоможіть знайти первісну
Приложения:
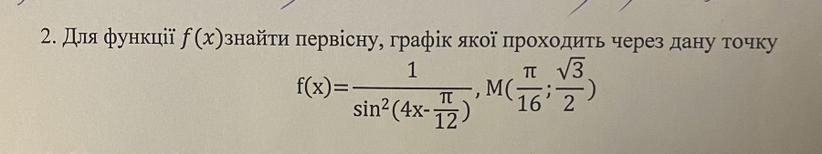
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Чтобы найти первообразную функцию , найдем неопределенный интеграл производной
:
По условию задачи:
Чтобы найти константу, подставим точки через которые проходит первообразная функция:
Тогда, первообразная функция будет выглядеть следующим образом:
Похожие вопросы
Предмет: Английский язык,
автор: anahitfrangyan
Предмет: Українська література,
автор: testbibra
Предмет: История,
автор: a2821
Предмет: Английский язык,
автор: evelinakhaerdinovaev
Предмет: Химия,
автор: madamd2017ovt5hw