Предмет: Геометрия,
автор: Yashin
Ребят, помогите пожалуйста!! Срочно!! Если решите эти 2 задачи получите еще пунктов.
За ранее спасибо!
Приложения:

Ответы
Автор ответа:
0
2) дано АВСДА1В1С!Д!-прямоугольный параллеллепипед, АВСД-квадрат, AB=4, B1D=8. Найти высоту параллелепипеда. Решение. по т. Пифагора ВД=√АВ²+АД²=√4²+4²=4√2, ΔДВВ! - прямоугольный. по т. Пифагора
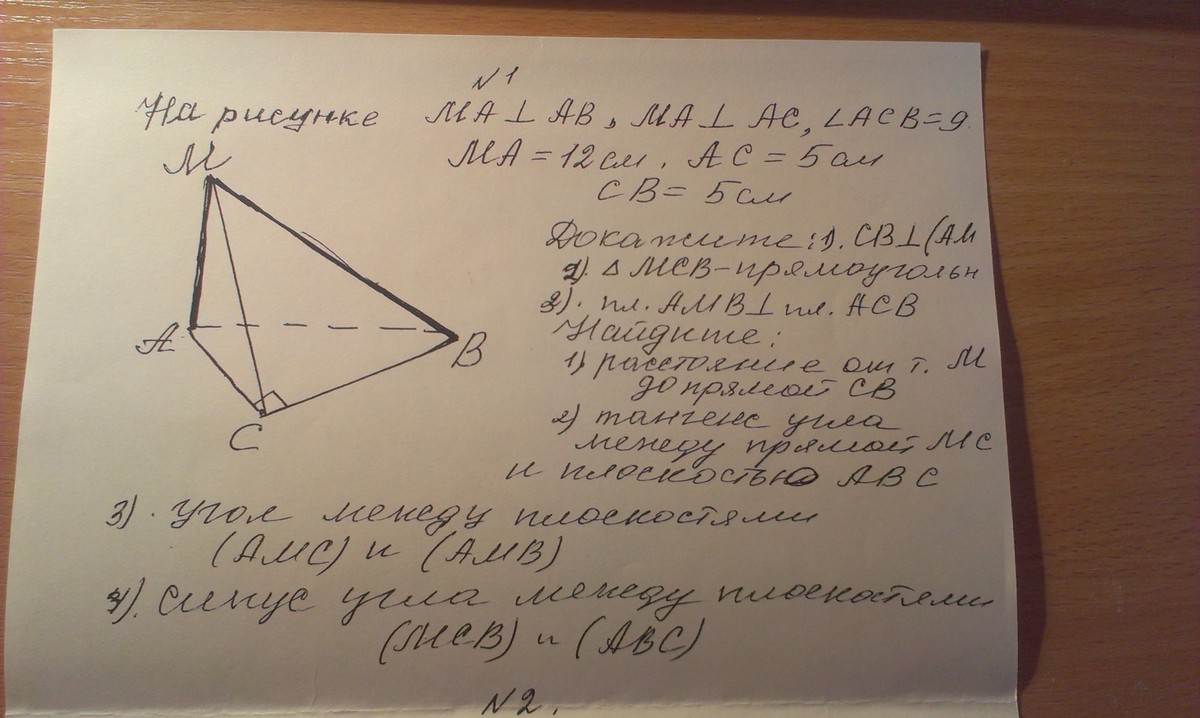
ВВ!=√ДВ!²-ДВ²=√8²-(4√2)²=√64-16*2=√32=4√2-высота параллелепипеда. Проведём диагональ боковой грани ДС! угол С!ДВ! - угол между диагональю и боковой гранью. ΔДС!В! - прямоугольный, В!С!=1/2В!Д, значит В!С! лежит против угла 30 градусов. 1) АМ перпендикулярна АВ, АМ перпендикулярна АС, значит АМ перпендикулярна плоскости АВС, тогда АМ перпендикулярна ВС. По ТТП МА перпендикулярна АС, АС перпендикулярна ВС, значит ВС перпендикулярна МС, и тогда ВС перпендикулярна плоскости АМС. 2) так как ВС перпендикулярна МС, то ΔМСВ - прямоугольный 3) АМ перпендикулярна плоскости АВС, значит плоскость АМВ перпендикулярна плоскости АВС. расстояние от точки М до прямой ВС=МС. ΔАМС-прямоугольный по т. Пифагора МС=√12²+5²=√169=13, tgMCA=AM/AC=12/5/. Угол между плоскостями АМС и АМВ= углу САВ. Так как ΔАСВ-прямоугольный, равнобедренный с основанием АВ, то угол А=углу В=45 градусов 4) sinACM=12/13
ВВ!=√ДВ!²-ДВ²=√8²-(4√2)²=√64-16*2=√32=4√2-высота параллелепипеда. Проведём диагональ боковой грани ДС! угол С!ДВ! - угол между диагональю и боковой гранью. ΔДС!В! - прямоугольный, В!С!=1/2В!Д, значит В!С! лежит против угла 30 градусов. 1) АМ перпендикулярна АВ, АМ перпендикулярна АС, значит АМ перпендикулярна плоскости АВС, тогда АМ перпендикулярна ВС. По ТТП МА перпендикулярна АС, АС перпендикулярна ВС, значит ВС перпендикулярна МС, и тогда ВС перпендикулярна плоскости АМС. 2) так как ВС перпендикулярна МС, то ΔМСВ - прямоугольный 3) АМ перпендикулярна плоскости АВС, значит плоскость АМВ перпендикулярна плоскости АВС. расстояние от точки М до прямой ВС=МС. ΔАМС-прямоугольный по т. Пифагора МС=√12²+5²=√169=13, tgMCA=AM/AC=12/5/. Угол между плоскостями АМС и АМВ= углу САВ. Так как ΔАСВ-прямоугольный, равнобедренный с основанием АВ, то угол А=углу В=45 градусов 4) sinACM=12/13
Похожие вопросы
Предмет: Биология,
автор: geraera79
Предмет: Английский язык,
автор: adeliyamosha
Предмет: География,
автор: BoldyirevaMariya
Предмет: Физика,
автор: NikaStrygina
Предмет: Алгебра,
автор: ЁжикКеша