Предмет: Математика,
автор: of3785698
Розв'язати нерівности (x-3)(5-x)(x+4)≥0
Ответы
Автор ответа:
1
Ответ:
**Розв'язання нерівності \((x-3)(5-x)(x+4) \geq 0\):**
1. **Знаходимо точки, де вираз дорівнює нулю:**
\((x-3) = 0\) при \(x = 3\),
\((5-x) = 0\) при \(x = 5\),
\((x+4) = 0\) при \(x = -4\).
2. **Розглядаємо інтервали між цими точками:**
- В інтервалі \((-\infty, -4)\) множники \((x+4)\) і \((x-3)\) від'ємні, а \((5-x)\) додатній.
- В інтервалі \((-4, 3)\) всі множники від'ємні.
- В інтервалі \((3, 5)\) множники \((x-3)\) і \((5-x)\) від'ємні, а \((x+4)\) додатній.
- В інтервалі \((5, \infty)\) всі множники додатні.
3. **Об'єднуємо інтервали, де вираз не менше нуля:**
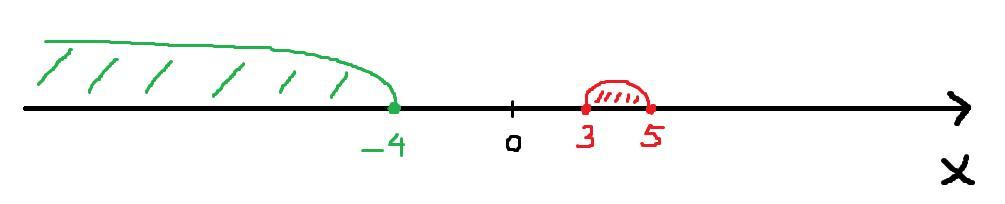
Розв'язок: \((-4 \leq x \leq 3) \cup (5 \leq x < \infty)\).
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: svyatiks19
Предмет: Информатика,
автор: u90136828
Предмет: История,
автор: srilivili
Предмет: Русский язык,
автор: nurtazinovaarina
Предмет: Литература,
автор: aigulikanova