Question

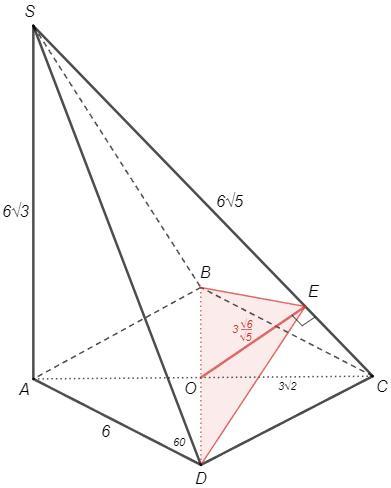
Основанием пирамиды SABCD является квадрат, а боковое ребро SА пер- пендикулярно плоскости основания. Найдите площадь сечения пирамиды плоскостью, проходящей через диагональ основания BD и перпендикуляр- ной ребру SC, если двугранный угол при ребре CD равен 60°, BD=6/2. 1) 3,2 √15; 2) 16; 3) 4 √15; 4)5√2; 5) 3,6 √15.
прошу о помощи ​

Answer 1

BD⊥AC (диагонали квадрата)

SA⊥(ABC), BD⊥AC => BD⊥SC (т о трех перпендикулярах)

Проведем OE⊥SC

SC⊥BD, SC⊥OE => SC⊥(BED)

△BED - искомое сечение

CE⊥(BED), OC⊥BD => OE⊥BD

OE - высота △BED

BD=6√2 => AD=6

SA⊥(ABC), AD⊥CD => SD⊥CD (т о трех перпендикулярах)

∠(SD;AD) =∠SCDA =60°

SA =AD tg60 =6√3

SA⊥(ABC)=> SA⊥AC

SC=√(SA^2+AC^2) =6√5

△OEC~△SAC => OE/SA=OC/SC => OE=3√2 *6√3 /6√5 =3√6/√5

S(BED) =1/2 BD*OE =1/2 *6√2 *3√6/√5 =18√3/√5 =3,6√15