Предмет: Математика,
автор: stellaichme
Знайти ліміт послідовності
Приложения:

Ответы
Автор ответа:
0
Ответ:
Предел последовательности .
Величина ограниченная , так как
, а ограниченная величина , умноженная на бесконечно малую , даёт бесконечно малую .
Приложения:
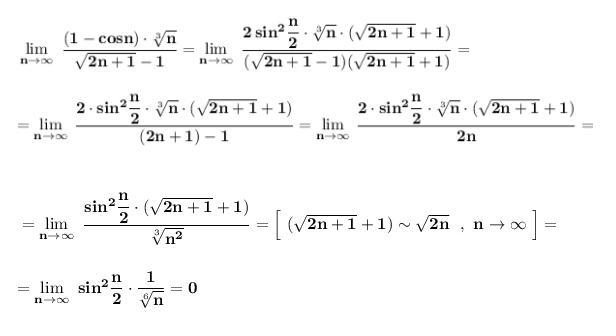
Похожие вопросы
Предмет: Математика,
автор: zarembadanil8
Предмет: Математика,
автор: lavrenyuk310111
Предмет: Математика,
автор: Аноним
Предмет: Немецкий язык,
автор: ksugl