Предмет: Алгебра,
автор: sasabelikova69
Будь ласка, дуже потрібно
Приложения:
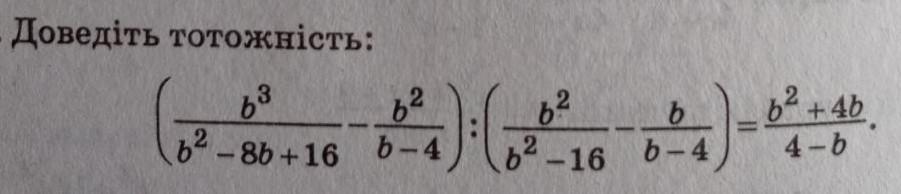
Ответы
Автор ответа:
0
Упростим левую часть тождества :
Тождество доказано
Автор ответа:
0
Відповідь:
Смотри фото
Пояснення:
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: mihailaliminari
Предмет: Қазақ тiлi,
автор: kissnozx
Предмет: Математика,
автор: karakatalipbek14
Предмет: Математика,
автор: MrsStefi
Предмет: Математика,
автор: serikhanovainkar