Предмет: Алгебра,
автор: kristinalutsenko76
Помогите пожалуйста решить
Приложения:
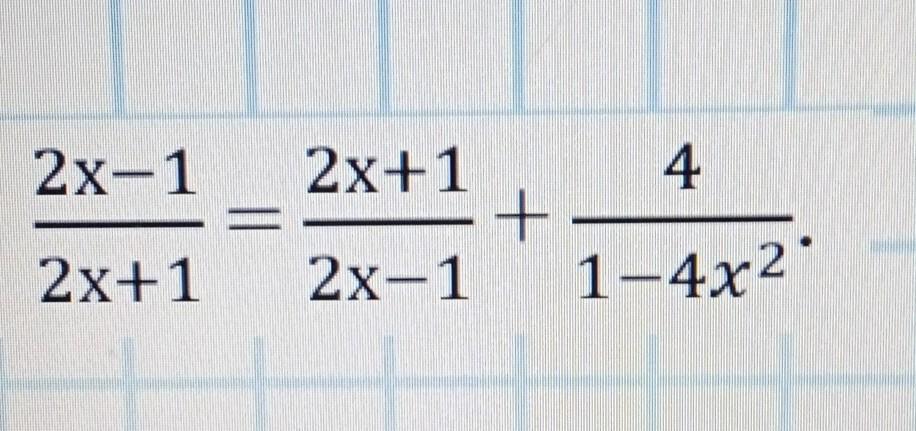
Ответы
Автор ответа:
0
Ответ : корней нет
Похожие вопросы
Предмет: Информатика,
автор: animalovisasu25
Предмет: Химия,
автор: topimtop46
Предмет: Математика,
автор: KonspekSezim
Предмет: Геометрия,
автор: kuaaa2005
Предмет: Английский язык,
автор: mariaalekseevnapetro