1)
Проведено n = 900 незалежних випробувань, в кожному з яких може відбутись
подія А з ймовірністю 0,8.
а) За локальною теоремою Муавра-Лапласа знайдіть ймовірність того, що подія А
настане No + 700 разів ( No – номер варіанта роботи).
б) За інтегральною теоремою Муавра-Лапласа знайдіть ймовірність того, що подія А
настане від 700 до No + 720 разів.
2)
Дискретна випадкова величина Х задана рядом розподілу. Побудувати многокутник
розподілу. Знайдіть математичне сподівання і дисперсію випадкової величини Х, середнє
квадратичне відхилення. Знайдіть функцію розподілу F(x) та побудуйте її графік.
3)Випадкова величина Х задана функцією розподілу F(x). Знайдіть щільність розподілу
f(x), ймовірність того, що Х прийме значення в інтервалі (α; β). Побудувати графіки функцій
F(x) і f(x).
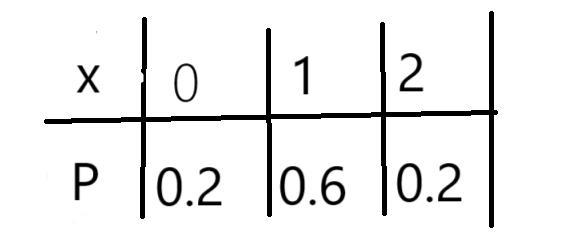
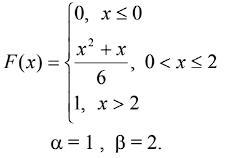
Ответы
1) а) Медіана біноміального розподілу з параметрами n і p дорівнює np. Отже, в даному випадку медіана дорівнює 0,8 * 900 = 720.
Тоді ймовірність того, що подія А настане 700 разів, дорівнює ймовірності того, що випадкова величина X, що має біноміальний розподіл з параметрами n = 900 і p = 0,8, прийме значення 700. Ця ймовірність дорівнює:
P(X = 700) = 0,5 * Φ(700 - 720 / √(900 * 0,8 * 0,2))
де Φ(x) - функція Лапласа.
P(X = 700) = 0,5 * Φ(-20 / √(72))
P(X = 700) ≈ 0,045
б) Інтегральна теорема Муавра-Лапласа стверджує, що для біноміального розподілу з параметрами n і p ймовірність того, що випадкова величина X прийме значення від a до b, дорівнює:
P(a ≤ X ≤ b) = 1 - Φ(b / √(n * p * q)) + Φ(a / √(n * p * q))
де Φ(x) - функція Лапласа, q = 1 - p.
У даному випадку a = 700 і b = 720. Отже, ймовірність того, що подія А настане від 700 до 720 разів, дорівнює:
P(700 ≤ X ≤ 720) = 1 - Φ(720 / √(900 * 0,8 * 0,2)) + Φ(700 / √(900 * 0,8 * 0,2))
P(700 ≤ X ≤ 720) = 1 - Φ(20 / √(72)) + Φ(-20 / √(72))
P(700 ≤ X ≤ 720) ≈ 0,9545 + 0,045
P(700 ≤ X ≤ 720) ≈ 0,9995