Question

ПОЖАЛУЙСТА, 40 БАЛЛОВ ПОМОГИТЕ РЕШИТЬ ЭТО!! Нужно вместе с полным решением

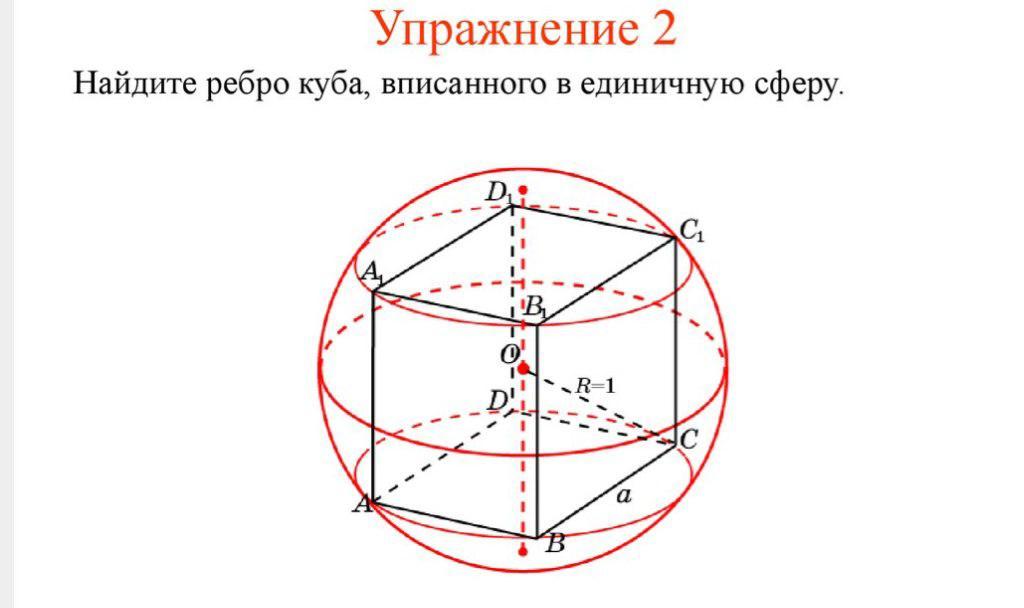
Найдите ребро куба, вписанного в единичную сферу

Answer 1

Ответ:

$\frac{2\sqrt{3}}{3}$ ─ самая правильная запись

Объяснение:

Точки A и $C_{1}$ образуют диагональ куба равную 2 ─ диаметр сферы, ведь радиус сферы равен 1, а отрезки AO і O$C_{1}$ равны как радиусы, а их сумма равна длинне A$C_{1}$.

d ─ диагональ куба

a ─ ребро куба

По формуле $d=a\sqrt{3}$ находим сторону куба, подставив значение d:

$2=a\sqrt{3}$

$4=3a^2$

$a^2=\frac{4}{3}$

$a=\sqrt{\frac{4}{3}}$

$a=\sqrt{\frac{4*3}{3*3} }$

$a=\sqrt{\frac{12}{9} }$

$a=\frac{\sqrt{12} }{\sqrt{9} }$

$a=\frac{\sqrt{4*3} }{\sqrt{3^2} }$

$a=\frac{\sqrt{2^2*3}}{3}$

$a=\frac{2\sqrt{3} }{3}$

Примечание:

Выше указанная формула это Теорема Пифагора для трёхмерных фигур:

$d^2=a^2+b^2+c^2$

У куба все стороны равны поэтому:

$d^2=a^2+a^2+a^2$

$d^2=3a^2$

$d=a\sqrt{3}$