Предмет: Математика,
автор: behramsmdov
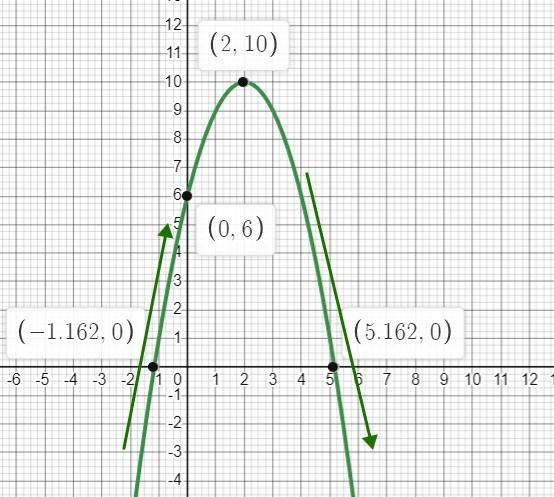
37) Для функции y= −2х2+4х + 6 определите: • направление ветвей соответствующей параболы; • точки пересечения с осями координат; • уравнение оси симметрии; • точку вершины; • наибольшее и наименьшее значения (если есть); • область определения и множество значений; • промежутки возрастания и убывания.
Помогите пожалуста очень важно
Приложения:

Ответы
Автор ответа:
1
Ответ:
в объяснении
Пошаговое объяснение:
y= -x² + 4x + 6
направление ветвей.
коэффициент при х² меньше 0, следовательно ветви направлены вниз
точки пересечения с осями координат
ось ОХ (у=0)
-x² + 4x + 6 = 0
ось OY (х=0)
у₁ = 6
точка вершины
точка (2; 10)
уравнение оси симметрии
х = 2
наибольшее и наименьшее значение
парабола ветвями вниз, значит она имеет максимум в точке вершины, минимум не ограничен снизу
область определения и множество значений
функция определена на всем пространстве х ∈ R.
значение изменяется у ≤ 10
D(y) = {x ∈ R}
E(y) = {y ∈ R: y≤ 10}
промежутки возрастания и убывания
функция возрастает на промежутке х ∈ (-∞; 2]
функция убывает на промежутке х ∈ [2; +∞)
Приложения:
behramsmdov:
Спасибо
ну это точный ответ?
Похожие вопросы
Предмет: Литература,
автор: berseerk
Предмет: Українська мова,
автор: sergiivnasasa210
Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Предмет: Биология,
автор: j2795326
Предмет: Математика,
автор: hikitov555