Предмет: Геометрия,
автор: dlo0kin13
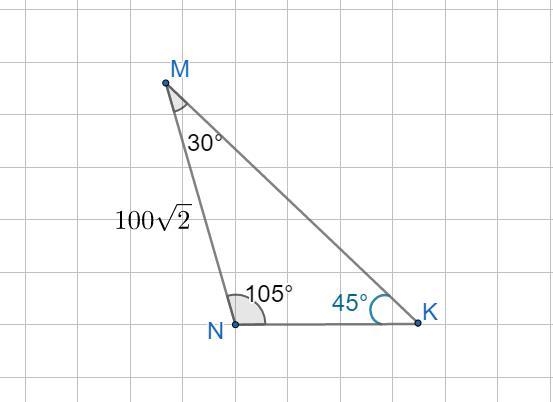
Дан треугольник MNK в котором MN=100√2, а углы M=30, N=105. Определи длинну наименьшей стороны треугольника.
Ответы
Автор ответа:
2
Ответ:
Наименьшая сторона треугольника MNK равна 100.
Объяснение:
Дан треугольник MNK в котором MN=100√2, а углы M=30°, N=105°. Определить длину наименьшей стороны треугольника.
Дано: ΔMNK; MN = 100√2; ∠M = 30°; ∠N=105°.
Найти: длину наименьшей стороны.
Решение.
1) Найдем ∠K в заданном треугольнике.
- Сумма углов треугольника равна 180°.
∠K = 180° - (30° + 105°) = 45°.
2) Определим наименьшую сторону треугольника MNK.
- В треугольнике против меньшего угла лежит меньшая сторона, против большего угла - большая сторона.
Так как наименьший угол в треугольнике MNK - это ∠M = 30°, то наименьшая сторона лежит против ∠M.
Наименьшей стороной в ΔMNK является сторона NK.
3) Чтобы найти длину стороны NK воспользуемся теоремой синусов.
- Стороны треугольника пропорциональны синусам противолежащих сторон.
Для ΔMNK:
;
Наименьшая сторона треугольника MNK равна 100.
#SPJ1
Приложения:
dlo0kin13:
Хотя нет 301!
Похожие вопросы
Предмет: Українська література,
автор: margaritalitvinova84
Предмет: Литература,
автор: veronica021707
Предмет: Українська мова,
автор: ania228330
Предмет: История,
автор: brawleraidtop
Предмет: История,
автор: TypoiChelovechik