Question

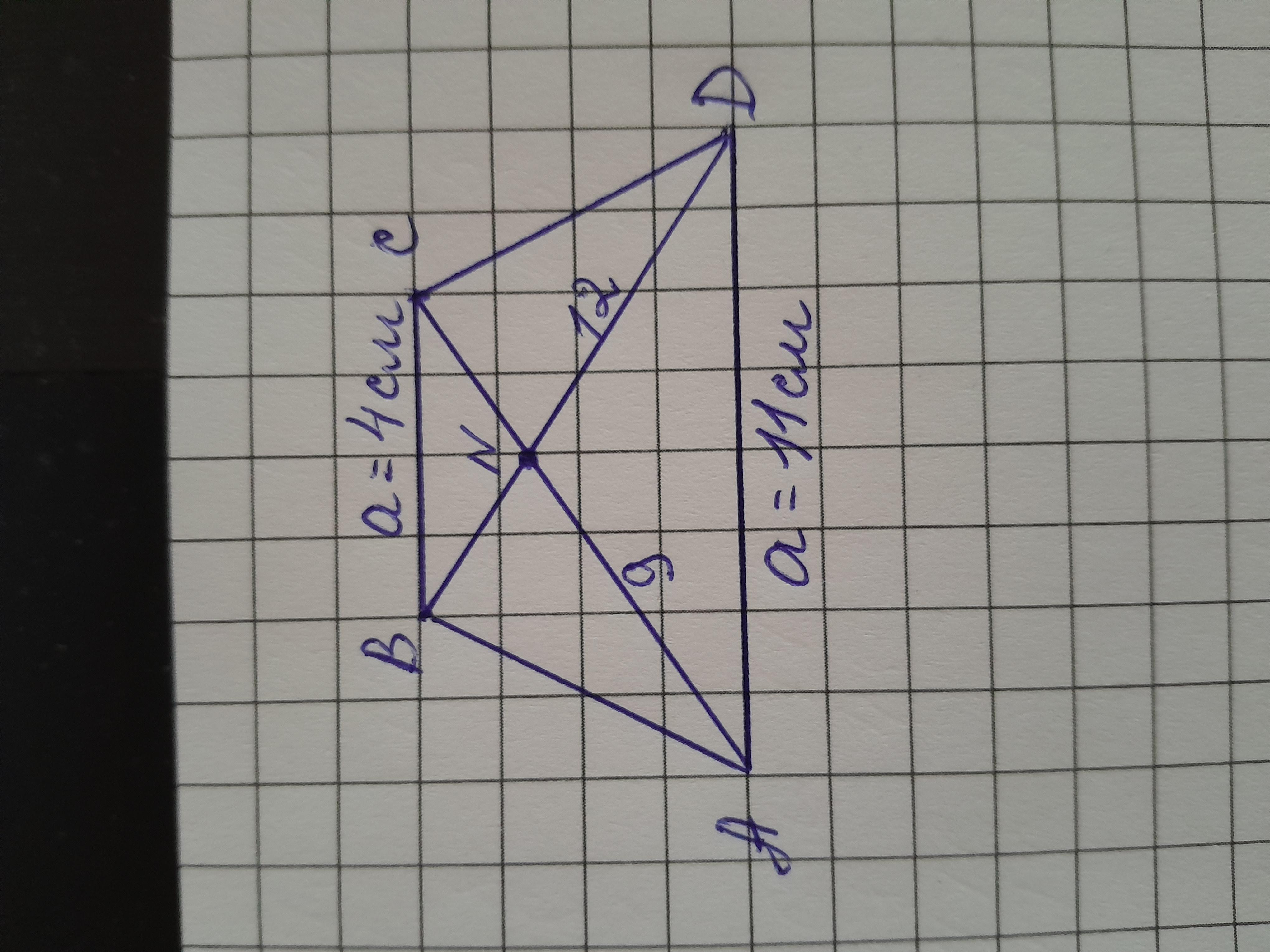
Знайдіть площу трапеції з основами 11 см і 4 см і діагоналями 9 см і 12 см.

Answer 1

Ответ:

Пошаговое объяснение:

При перетинанні діагоналями  трапеції утворюються подібня трикутники. Тоді маємо свідношення основ 4/11, і так діагоналі в точці перетину діляться у співвідношенні 4 : 11

4 + 11 = 15 частин

Знайдемо з пропорцій сторони трикутників

9/15 * 4 = 2,4 см

9/15 * 11 = 6,6 см

12/15 * 4 = 3,2 см

12 - 3,2 = 8,8 см

Обчислимо площу трикутників зі сторонами 4см; 3,2см; 2,4 см та 11см; 6,6см; 8,8 см.

Полупериметр дорівнює:

р = 1/2(а + b + c)

p₁ = 1/2 * (4 + 3,2 + 2,8) = 4,8 см

р₂ = 1/2 * ( 11 + 6,6 + 8,8) = 13,2 см

За формулою Герона знаходимо площу

S = √p(p - a) (p - b) (p - c)

S₁ = √4,8 * (4,8 - 4) * (4,8 - 3,2) * (4,8 - 2,8) = √4,8 * 0,8 * 1,6 * 2 =  3,84 см²

S₂ = √13,2 * (13,2 - 11) * (13,2 - 6,6) * (13,2 - 8,8) =

= √13,2 * 2,2 * 6,6 * 4,4 =  29,04 см²

Знаходимо висоту трикутника:

S = 1/2 a * h ⇒ h = S/(1/2а)

h₁ = 3,84/(1/2 * 4) = 1,92 см

h₂ = 29,04/(1/2 * 11) = 5,28 см

h = h₁ + h₂ = 1,92 + 5,28 = 7,2 см

Обчислюємо площу трапеції

S = 1/2 a * h = 1/2(4 + 11) * 7,2 = 54 см²