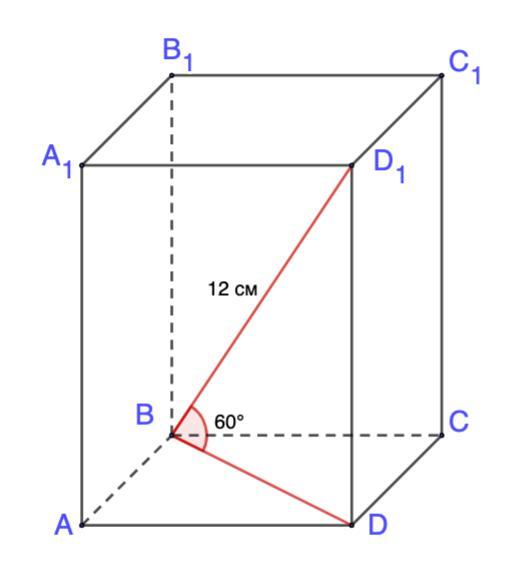
Дана правильная четырехугольная призма ABCDA,B C D . Диагональ BD, равна 12 см и составляет с основанием ABCD угол 60°. Найдите площадь полной поверхности призмы.

Ответы
Ответ:
Площадь полной поверхности призмы равна (72√6 + 36) см².
Объяснение:
Дана правильная четырехугольная призма ABCDA₁B₁C₁D₁. Диагональ BD₁ равна 12 см и составляет с основанием ABCD угол 60°. Найдите площадь полной поверхности призмы.
Дано: ABCDA₁B₁C₁D₁ - правильная четырехугольная призма;
BD₁ = 12 см - диагональ призмы;
∠D₁BD = 60°.
Найти: Sпп - ?
Решение:
- Площадь полной поверхности призмы равна:
Sпп = Sбок + 2Sосн
Рассмотрим ΔD₁BD - прямоугольный.
∠D₁BD = 60°.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠ВD₁D = 90° - 60° = 30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ BD = BD₁ : 2 = 6 (см)
- Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
⇒ DD₁ = BD₁² - BD²
DD₁² = 144 - 36 = 108 ⇒ DD₁ = 6√3 см
- В основании правильной четырехугольной призмы лежит квадрат.
Пусть сторона квадрата равна а.
Рассмотрим ΔABD - прямоугольный.
По теореме Пифагора:
⇒ BD² = a² + a²
2a² = 36 ⇒ a² = 18 ⇒ a = 3√2 см
- Площадь квадрата равна квадрату его стороны.
S(ABCD) = a² = 18 см²
- Площадь боковой поверхности равна:
Sбок = Росн · Н,
где Росн - периметр основания; Н - высота призмы.
Росн = 3√2 · 4 = 12√2 (см)
Sбок = 12√2 · 6√3 = 72√6 (см²)
⇒ Sпп = 72√6 + 18 · 2 = 72√6 + 36 (см²)
#SPJ1