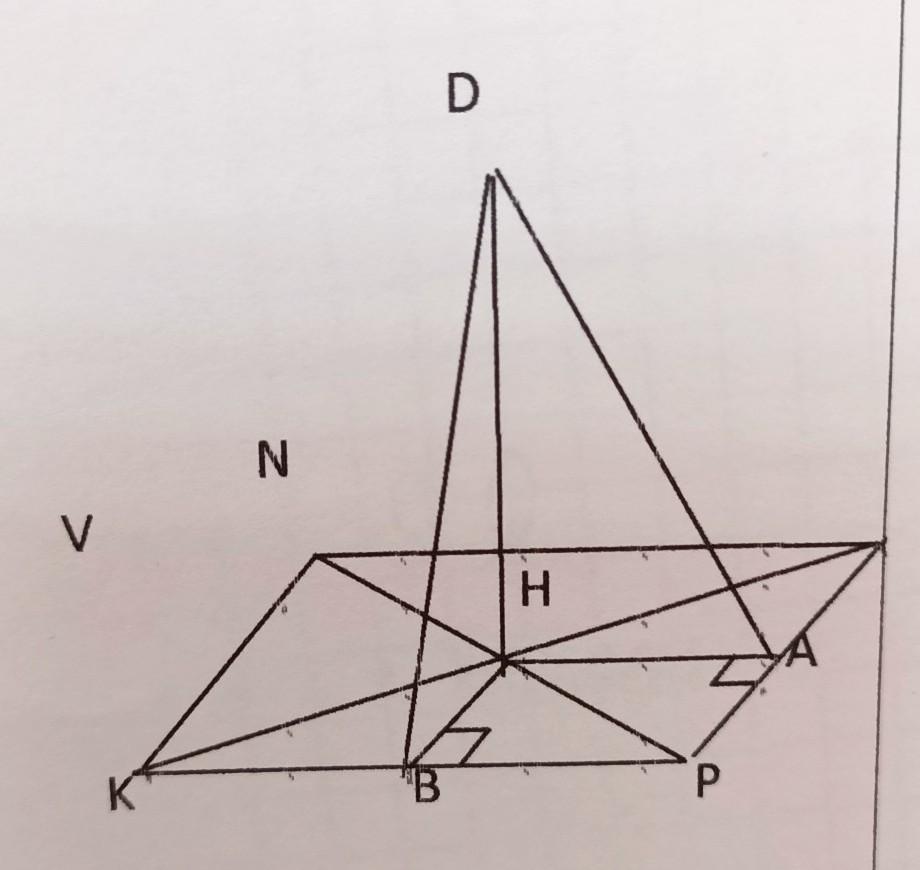
3. Через точку пересечения диагоналей прямоугольника KNVP проведен перпендикуляр DН к его плоскости, равный 12 см. Найдите расстояния от точки В до сторон прямоугольника, если его стороны равны 18 см и 10 см.
Ответы
Чтобы найти расстояния от точки В до сторон прямоугольника, нужно разделить прямоугольник на два треугольника и посчитать расстояния от точки В до оснований этих треугольников.
Для начала найдем расстояние от точки В до основания прямоугольника AB, где AB = 18 см и BC = 10 см.
Расстояние от точки В до основания АВ можно найти, используя теорему Пифагора. Поскольку точка B находится на расстоянии 12 см от плоскости прямоугольника, то она составляет с основанием АВ прямой угол.
По теореме Пифагора получаем:
BV² = AB² - dN²
BV² = (18 см)² - (12 см)²
BV² = 324 см² - 144 см²
BV² = 180 см²
BV = √180 ≈ 13.416 см
Таким образом, расстояние от точки В до основания АВ прямоугольника составляет примерно 13.416 см.
Теперь найдем расстояние от точки В до основания ВС прямоугольника.
Расстояние от точки В до основания ВС можно найти таким же образом, используя теорему Пифагора. Теперь основание ВС составляет прямой угол с прямой, проходящей через точку В и перпендикулярной плоскости прямоугольника.
BV² = BC² - dN²
BV² = (10 см)² - (12 см)²
BV² = 100 см² - 144 см²
BV² = -44 см²
Поскольку результат получился отрицательным, это означает.