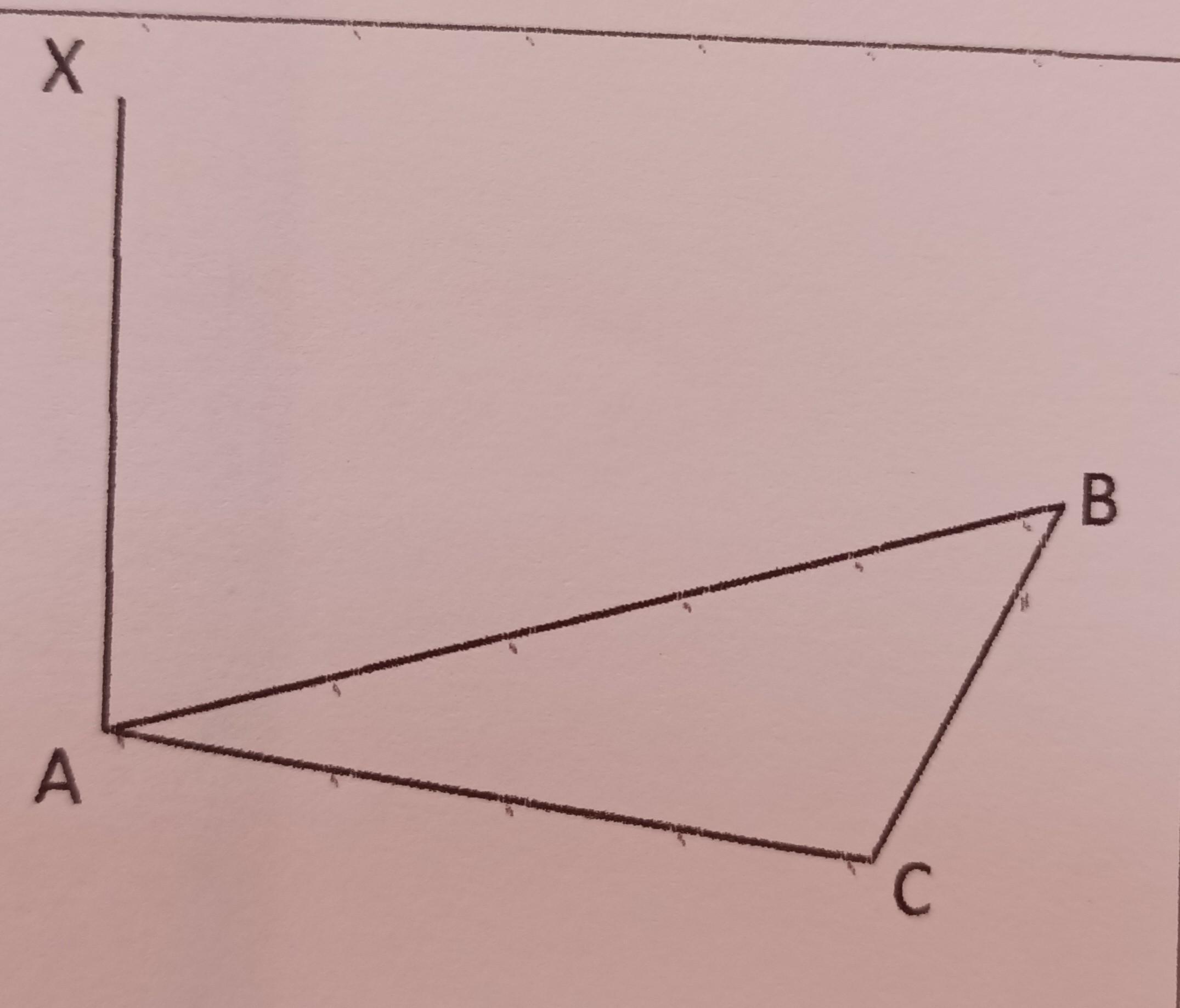
Отрезок ХА перпендикулярен плоскости прямоугольного △АВС
(∠ACB=90°).
а) Через точку Х проведите перпендикуляр к прямой ВС.
б) Найдите расстояние от точки Х до прямой ВС, если ХА = 16 см, АВ = 15 см, ВС = 9 см.
Ответы
а) Чтобы провести перпендикуляр к прямой ВС через точку Х, нам нужно найти направляющий вектор прямой ВС.
Вектор ВС можно найти, вычитая координаты точек В и С: ВС = (Сx - Вx, Сy - Вy, Сz - Вz).
Теперь, чтобы найти перпендикулярный вектор, мы должны поменять местами первые две координаты у вектора ВС и умножить одну из них на -1, чтобы поменять его направление. Таким образом, перпендикулярный вектор будет иметь координаты (-Сy + Вy, Сх - Вх, Сz - Вz).
б) Пусть точка Х имеет координаты (x,y,z), и чтобы найти расстояние от точки Х до прямой ВС, мы можем использовать формулу:
расстояние = |(х - Вx)(Сх - Вх) + (у - Вy)(Cy - By) + (z - Вz)(Сz - Вz)| / √((Сх - Вх)^2 + (Су - Ву)^2 + (Сz - Вz)^2).
Вставим известные значения в эту формулу, учитывая, что векторы ВС и HA перпендикулярны друг другу:
расстояние = |(х - Вx)(Вz - Сz) + (у - Ву)(Вх - Сх) + (z - Вz)(Ву - Су)| / √((Вz - Сz)^2 + (Вх - Сх)^2 + (Ву - Су)^2).
Подставим значения:
расстояние = |(х - 0)(9 - 0) + (у - 0)(15 - 0) + (z - 0)(0 - 0)| / √((9 - 0)^2 + (15 - 0)^2 + (0 - 0)^2)
= |9x + 15y| / √(81 + 225)
= |9x + 15y| / √306.
Ответ: Расстояние от точки Х до прямой ВС равно |9x + 15y| / √306.