Предмет: Математика,
автор: katiasv333
Знайти границю функції, не користуючись правилом Лопітоля.
хелп...
Приложения:
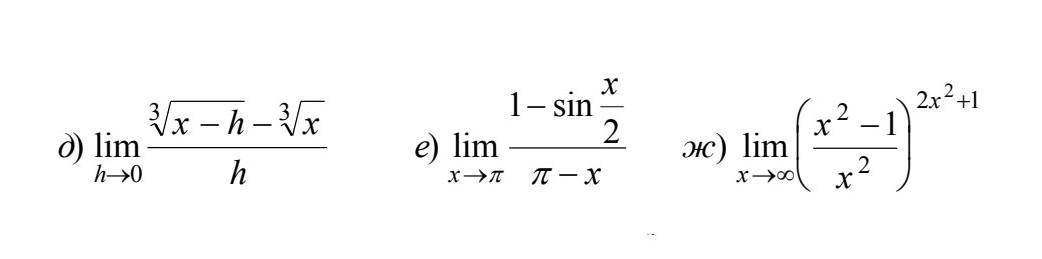
Ответы
Автор ответа:
2
Ответ:
Вычислить пределы функций .
1) Домножаем числитель и знаменатель дроби на выражение , сопряжённое числителю .
2) Заменяем бесконечно малые величины эквивалентными .
3) Вторoй замечательный предел :
Приложения:
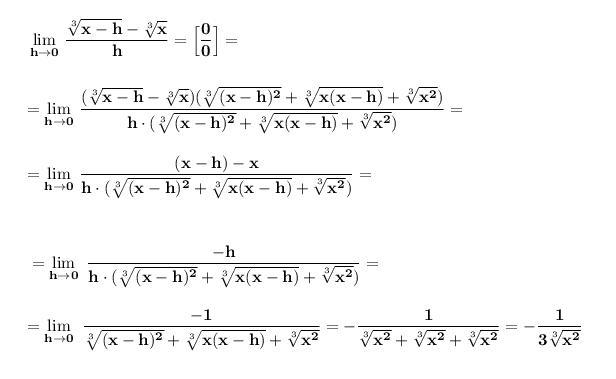
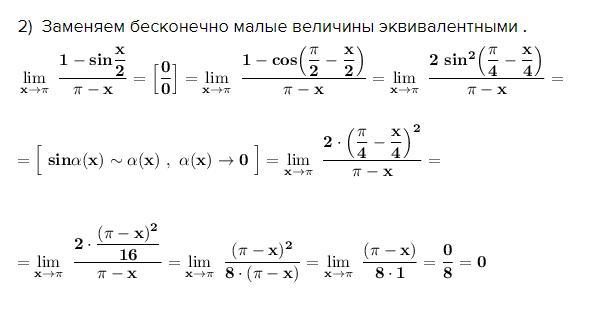
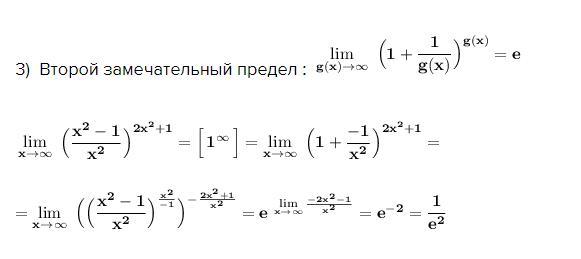
Похожие вопросы
Предмет: Математика,
автор: pradkamaksim443
Предмет: Математика,
автор: strahanzhela
Предмет: Английский язык,
автор: doramidoraemon47
Предмет: Право,
автор: ruslan010906
Предмет: Қазақ тiлi,
автор: maksatulyanuarbek54