Предмет: Алгебра,
автор: yassiikss
СРОЧНО ДАЮ 100 БАЛІВ АЛГЕБРА 8 КЛАС
Приложения:
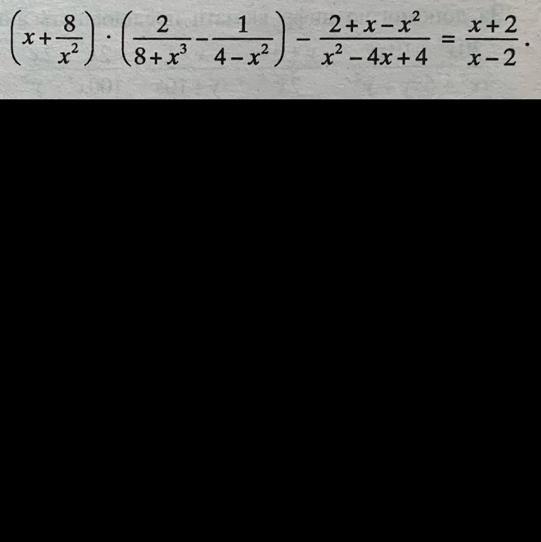
Ответы
Автор ответа:
0
Объяснение:
Автор ответа:
1
Ответ:
Доказать тождество . Применяем формулы сокращённого умножения .
Тождество доказано .
Приложения:
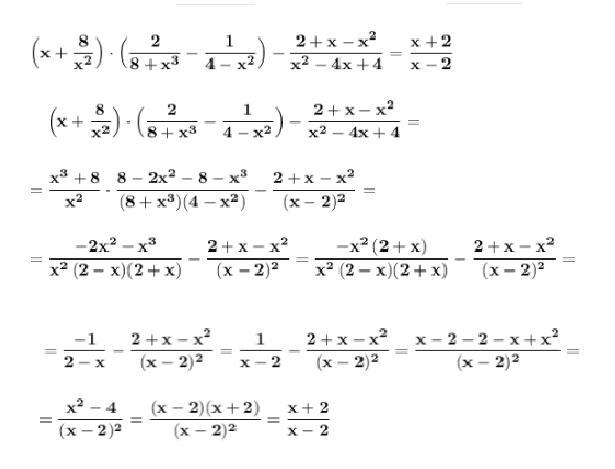

Похожие вопросы
Предмет: Українська література,
автор: karishallllllllllll
Предмет: Химия,
автор: kurisenkoalona
Предмет: Українська мова,
автор: do752167899
Предмет: Қазақ тiлi,
автор: serikkazyaruzhan