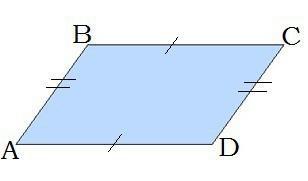
Знайти кути паралелограма, якщо два його кути відносяться як 4:5
Ответы
Ответ:
В паралелограмі протилежні кути рівні між собою. Тому, якщо два кути паралелограма відносяться як 4:5, значить, що і два протилежні кути відносяться так само.
Нехай перший кут дорівнює 4x, де x - коефіцієнт пропорційності.
Тоді другий кут дорівнює 5x.
Таким чином, сума цих двох кутів дорівнює 4x + 5x = 9x.
У паралелограмі сума всіх кутів дорівнює 360 градусів.
Тому, оскільки паралелограм має два пари рівних кути, можемо записати рівняння: 9x + 9x = 360.
Розв'язуємо рівняння:
18x = 360,
x = 20.
Отже, перший кут дорівнює 4 * 20 = 80 градусів, а другий кут дорівнює 5 * 20 = 100 градусів.
Отже, кути паралелограма дорівнюють 80 градусів і 100 градусів.
Объяснение:
Дано: ∠А/∠B = 4/5
Знайти ∠A, ∠B, ∠C, ∠D
Розв'язання
Нехай x – коефіцієнт пропорційності
∠A=4х, ∠B=5х
За властивістю паралелограма:
∠A + ∠B = 180°
4х + 5х = 180°
9х = 180°
x = 20
∠A=∠C= 4×20 = 80°
∠B = ∠D = 5 × 20 = 100°
Відповідь: 80°, 100°, 80°, 100°.