Предмет: Алгебра,
автор: utemis06
8.4 (в,г)! Даю 100 баллов
Приложения:

Ответы
Автор ответа:
0
Ответ:
Решить тригонометрическое уравнение .
Применяем формулу синуса двойного угла и основное тригономет- рическое тождество :
Приложения:
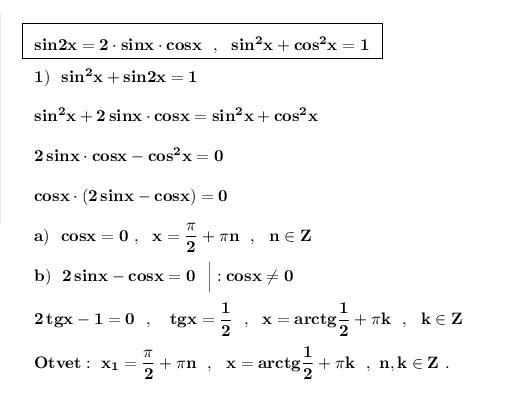
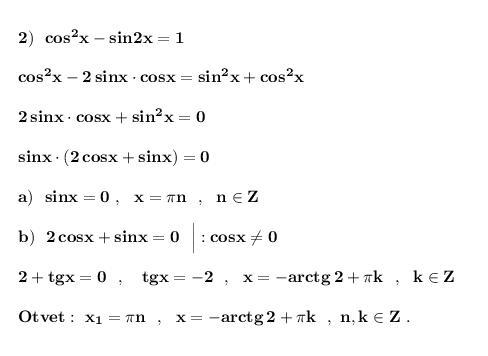
Похожие вопросы
Предмет: Литература,
автор: 0w0Dmytro
Предмет: Математика,
автор: anastasiaturbal23
Предмет: Литература,
автор: triksimorohovskaa
Предмет: История,
автор: Аноним