Предмет: Геометрия,
автор: annazaezc
АВСD – прямокутна трапеція з периметром 54 см. Коло, що вписано в цю трапецію, ділить точкою дотику більшу бічну сторону на відрізки довжиною 12 см та 3 см. Визнач радіус вписаного кола.
Ответы
Автор ответа:
4
Ответ:
Радиус вписанной окружности равен 6 см.
Объяснение:
АВСD-прямоугольная трапеция с периметром 54 см. Окружность, вписанная в эту трапецию, делит точкой касания большую боковую сторону на отрезки длиной 12 см и 3 см. Определи радиус вписанной окружности.
Дано: ABCD - прямоугольная трапеция;
Р(ABCD) = 54 см;
Окр. (О;R) - вписана в ABCD;
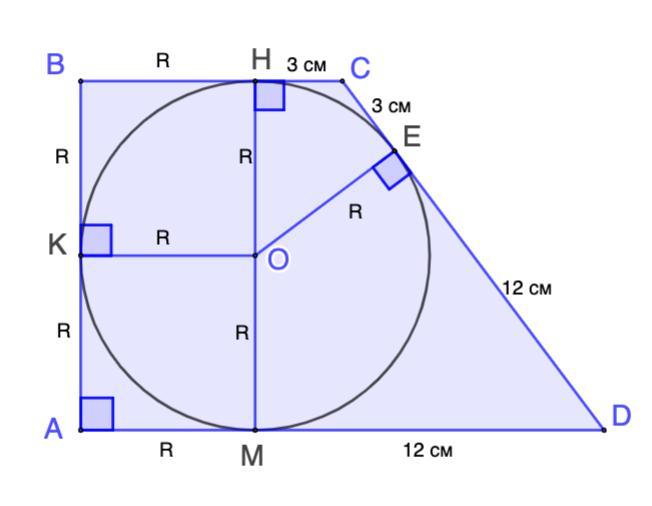
СЕ = 3 см, ЕD = 12 см, Е - точка касания.
Найти: R.
Решение:
- Периметр - сумма длин всех сторон.
⇒ P(ABCD) = АВ + ВС + CD + AD = 54см
- Отрезки касательных к окружности, проведенных из одной точки, равны.
⇒ СН = СЕ = 3 см; ED = DM = 12 см;
- Радиус, проведенный в точку касания, перпендикулярен касательной.
⇒ КВНО и АКОМ - квадраты.
ВН = ВК = R; AK = AM = R
⇒ P(ABCD) = 2R + (R+3) + (3+12) + (12+R) = 54 cм
4R + 30 = 54
4R = 24 |:4
R = 6
⇒ Радиус вписанной окружности равен 6 см.
#SPJ1
Приложения:
Похожие вопросы