Question

в прямоугольнике АВСD со сторонами АВ=2, ВС=5 случайно выбирают точку. найти вероятность того что она расположена ближе к вершине А, чем к точке пересечения диагоналей. С решением плз

Answer 1

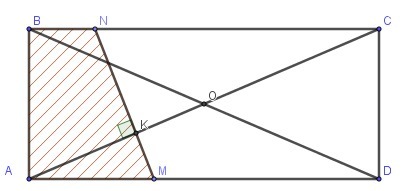
Проведем серединный перпендикуляр к АО. Из прямоугольного треугольника ACD по теореме Пифагора

$AD=sqrt{2^2+5^2}=sqrt{29}$

$AK=OK=frac{1}{2}AO=frac{1}{4}AC=frac{sqrt{29}}{4}$

Треугольники AKM и ACD подобны по двум углам (∠AKM = ∠ADC и ∠А - общий).

AM/AK = AC/AD  ⇒  AM=29/20

Треугольники AKM и NKC подобны по двум углам (∠AKM=∠CKN и ∠KAM = ∠NCK как накрест лежащие при BC || AD и секущей AC).

AM/AK = NC/CK = (BC-BN)/(AC-AK) ⇒ BN = 13/20

Площадь четырехугольника ABNM: $S_1=dfrac{BN+AM}{2}cdot AB=dfrac{dfrac{13}{20}+dfrac{29}{20}}{2}cdot2=dfrac{21}{10}$

Площадь прямоугольника ABCD: $S_2=ABcdot BC=2cdot5=10$

Искомая вероятность по геометрической формуле вероятности:

$P=dfrac{S_1}{S_2}=dfrac{dfrac{21}{10}}{10}=dfrac{21}{100}=0.21$

Ответ: 0,21.