Предмет: Алгебра,
автор: ruslangla
прошу порівняти х і у
Приложения:
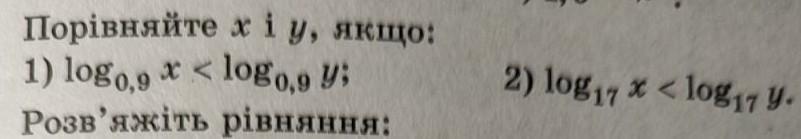
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Свойство логарифмических неравенств:
Решение. Применим свойства логарифмических неравенств.
#SPJ1
ruslangla:
жалб, что не раньше (( уже все((
Похожие вопросы
Предмет: История,
автор: p2504333
Предмет: Английский язык,
автор: ilushaklusa
Предмет: Геометрия,
автор: Davaa122222
Предмет: Химия,
автор: Natali2119
Предмет: Английский язык,
автор: alinaknyazkina9