Предмет: Алгебра,
автор: 66667777pop
Нужно срочно решить 3 примера с алгебры!
Приложения:
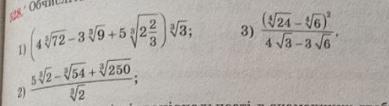
Ответы
Автор ответа:
1
Ответ:
Действия с корнями .
Приложения:
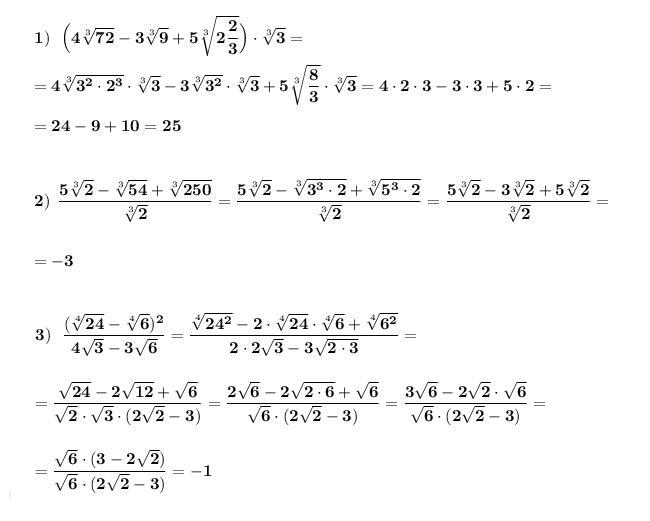
Похожие вопросы
Предмет: Математика,
автор: telliabdullaeva
Предмет: Геометрия,
автор: denkorc19
Предмет: Физика,
автор: deniskobzistyj749
Предмет: Оʻzbek tili,
автор: Аноним