Предмет: Математика,
автор: pazhun2007
Поможіть будь-ласка дам 50 балів
Приложения:
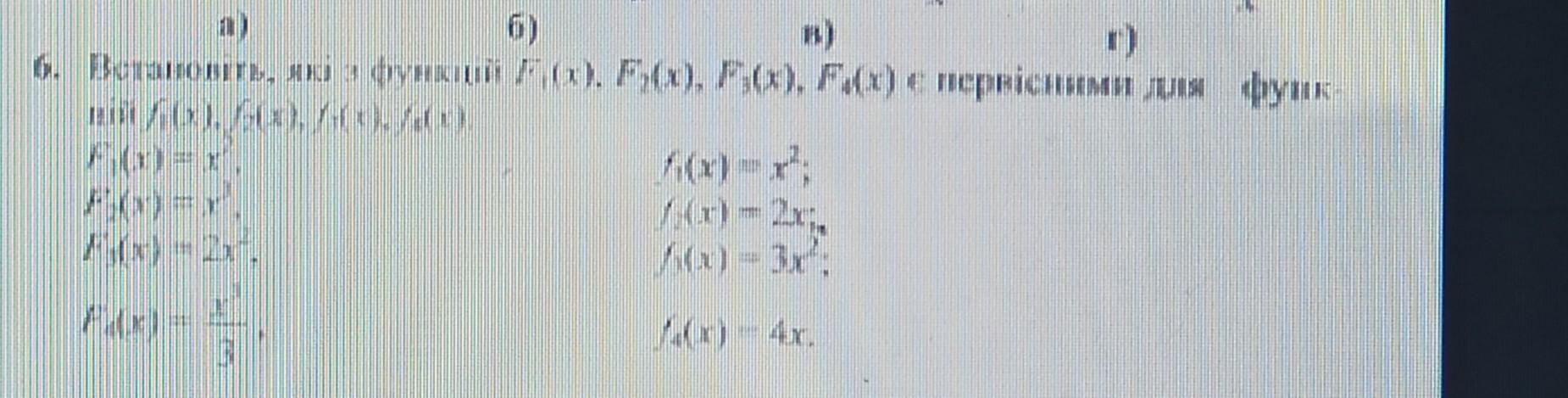
Ответы
Автор ответа:
0
Ответ:
Если F(x) - первообразная для функции f(x) , то .
Проверим это .
Можно найти первообразные для функций f(x) .
Похожие вопросы
Предмет: Математика,
автор: kairgeldinovanazimdy
Предмет: Алгебра,
автор: Horande
Предмет: История,
автор: 0AngeliIi6nkarrrR0
Предмет: Обществознание,
автор: dfghgj