Предмет: Математика,
автор: ichbinyura
Помогите решить, 45 баллов
Приложения:
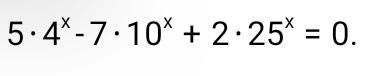
Ответы
Автор ответа:
0
Ответ:
поделим уравнение на 2 ^(2х)
ответ
х=0
х=1
Похожие вопросы
Предмет: Математика,
автор: sergiugolovkov29
Предмет: Українська література,
автор: bao262010
Предмет: Физика,
автор: anarmetovaferuzkaa
Предмет: Химия,
автор: marikoks
Предмет: Биология,
автор: arishka20142