Предмет: Математика,
автор: byvalinmaksim194
найти производную а) и г)
Приложения:
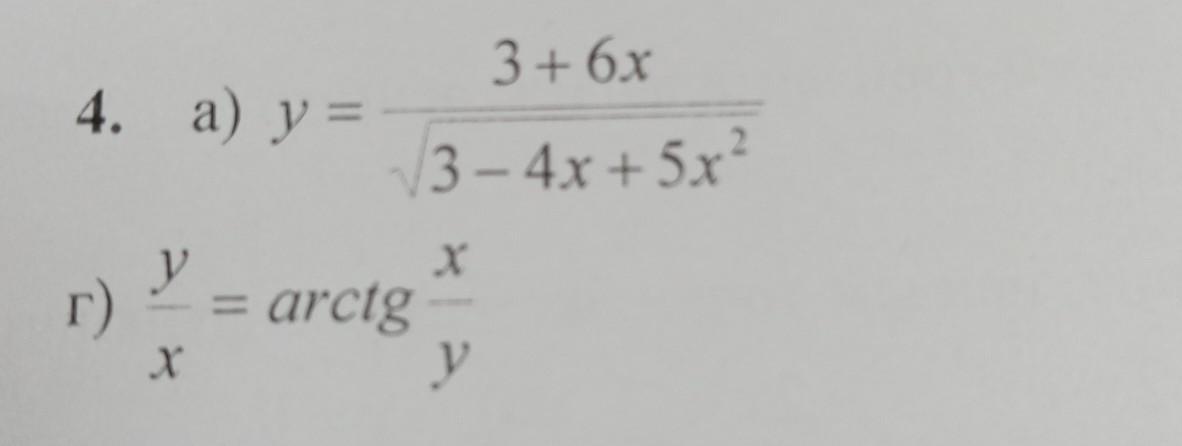
Ответы
Автор ответа:
0
Ответ:
Найти производные функций .
Формулы : .
Приложения:

Похожие вопросы
Предмет: География,
автор: marina835740
Предмет: География,
автор: marina835740
Предмет: География,
автор: marina835740
Предмет: Русский язык,
автор: aleksasasa67
Предмет: География,
автор: anastasiaxbutko