Question

....................................

Answer 1

Ответ:

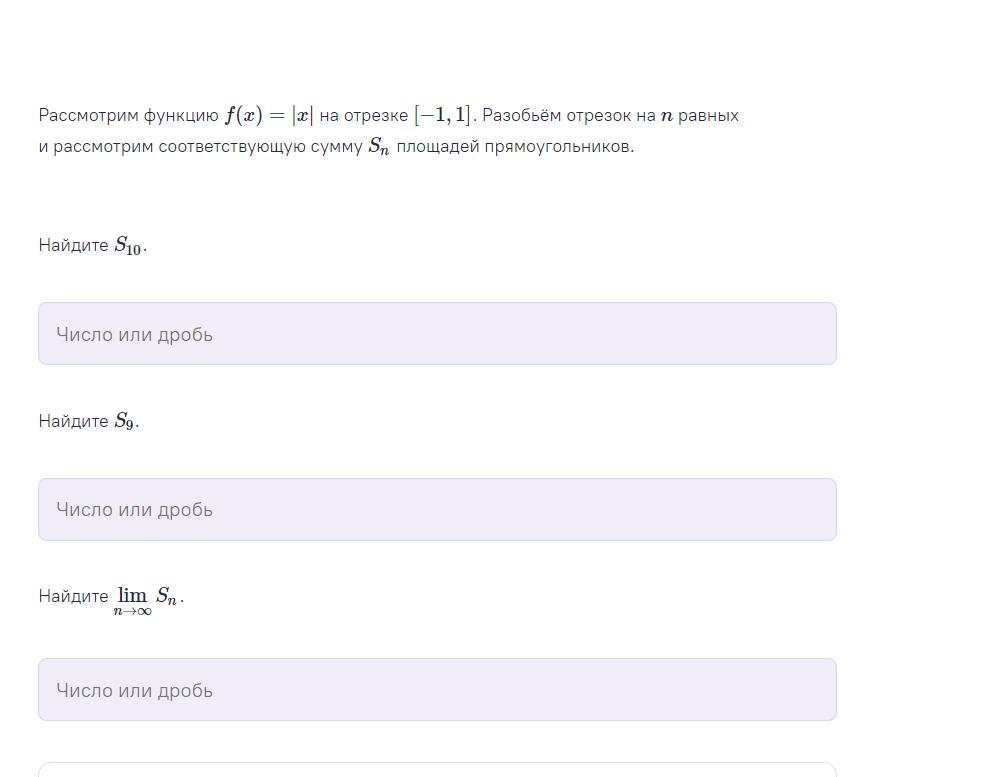
1; 82/81; 1.

Объяснение:

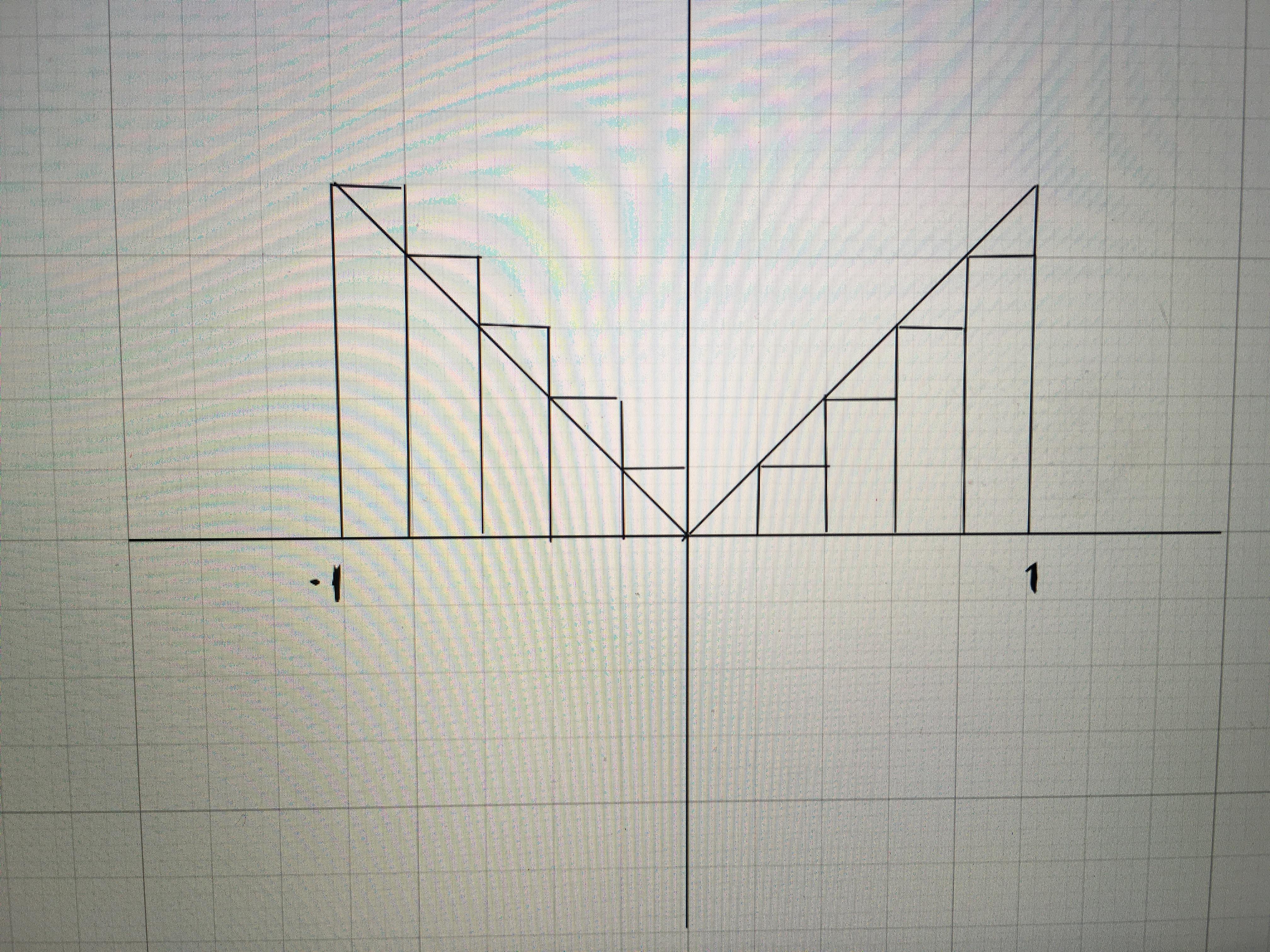
На первой картинке рассматривается случай n=10 (для любого чётного n=2k картинка будет аналогичной). Мы видим, что в половине случаев (при x<0) прямоугольники, покрывая область под графиком, вылезают за её пределы в виде пяти (в общем случае n/2=k) одинаковых треугольников, а при x>0 прямоугольники покрыли не всю область под графиком, оставив непокрытыми такие же пять (в общем случае n/2=k)  треугольников. Поэтому сумма площадей прямоугольников (на математическом языке - интегральная сумма) равна площади под графиком, то есть равна 1.

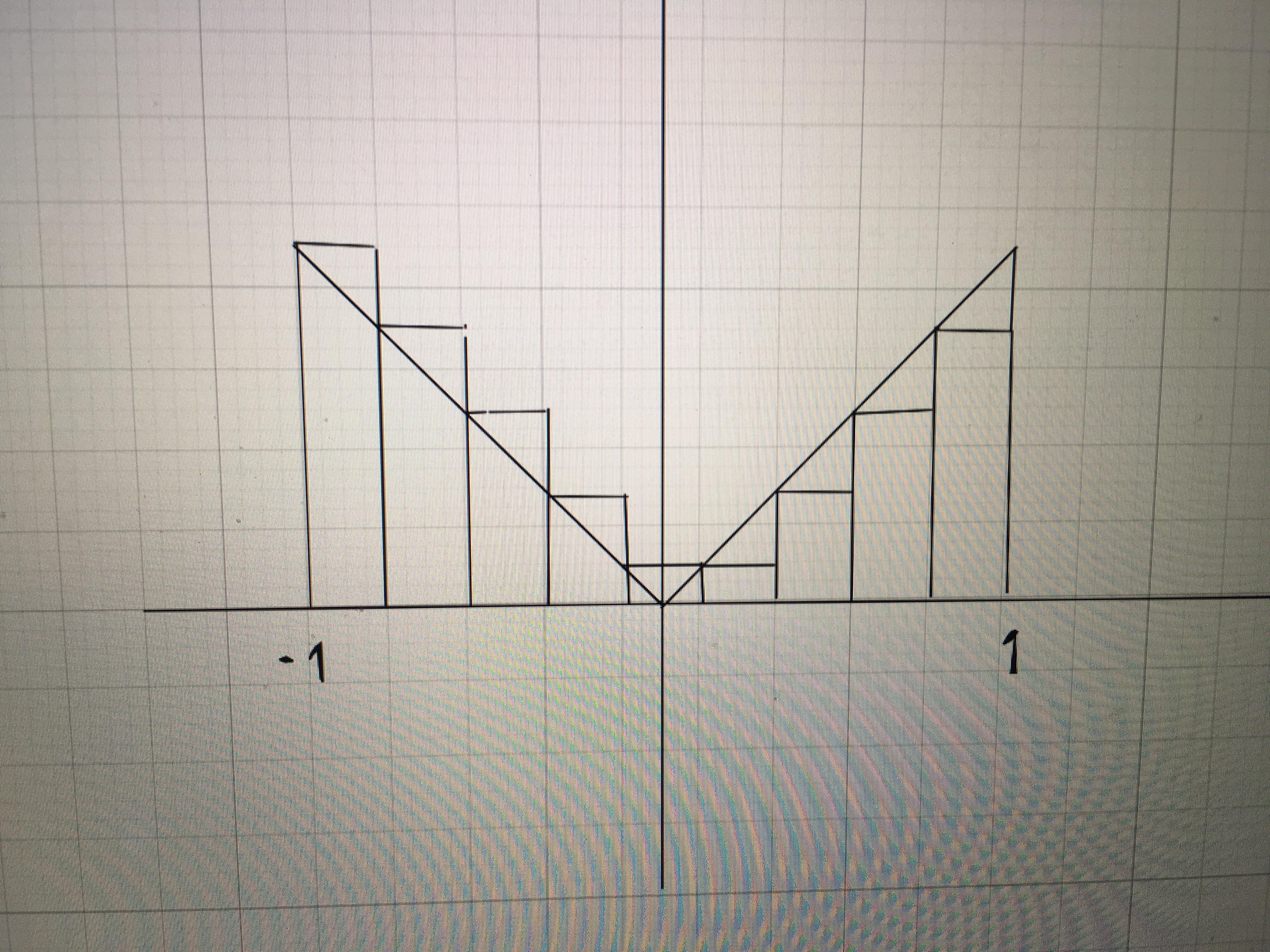
На второй картинке рассматривается случай n=9 (для любого нечетного n=2k+1 картинка будет аналогичной). Четыре треугольника слева компенсируют четыре треугольника справа (в общем случае (n-1)/2=k треугольников). Остается только средний треугольник, который вылезает за пределы графика, его основание равно 2/9, высота равна 1/9, площадь равна 1/9² (в общем случае 2/n, 1/n и 1/n² соответственно).

Вывод: $S_{10}=1;\ S_9=1+1/81=82/81.$

В общем случае $S_{2k}=1;\ S_{2k+1}=1+\dfrac{1}{(2k+1)^2}.$

Поэтому ответ с пределом очевиден: он равен 1 (и равен площади под графиком функции).