Помогите решить 3 задачи , дам 50 баллов

Ответы
Ответ:
3) АВCD- трапеция , ВС || AD , ВС =2 , ВН и СК - высоты ⇒
BН || CK , значит ВСНК - прямоугольник и ВС = НК = 2 .
Так как по условию ВН = ВС , а ВН = СК как противоположные стороны прямоугольника , то СК = 2 .
∠CDK = 45° , Δ CDK - прямоугольный ⇒ ∠DCK = 45° ⇒
Δ CDK - равнобедренный и СК = КD = 2 .
AD = AH + KH + KD = 3 + 2 + 2 = 7
4) АВCD- трапеция , ВС || AD , по условию ВС = AB ⇒
Δ АВС - равнобедренный и ∠ВАС = ∠ВСА .
Δ АСD - прямоугольный , ∠АСD = 90° , ∠ADC = 60° по условию ⇒
∠САD = 90°- 60° = 30°
∠BCA = ∠CAD = 30° как внутренние накрест лежащие углы при
BC || AD и секущей АС .
Рассмотрим Δ АВС , ∠B = 180° - ∠ВАС - ∠ВСА = 180°° - 30°- 30° = 120°
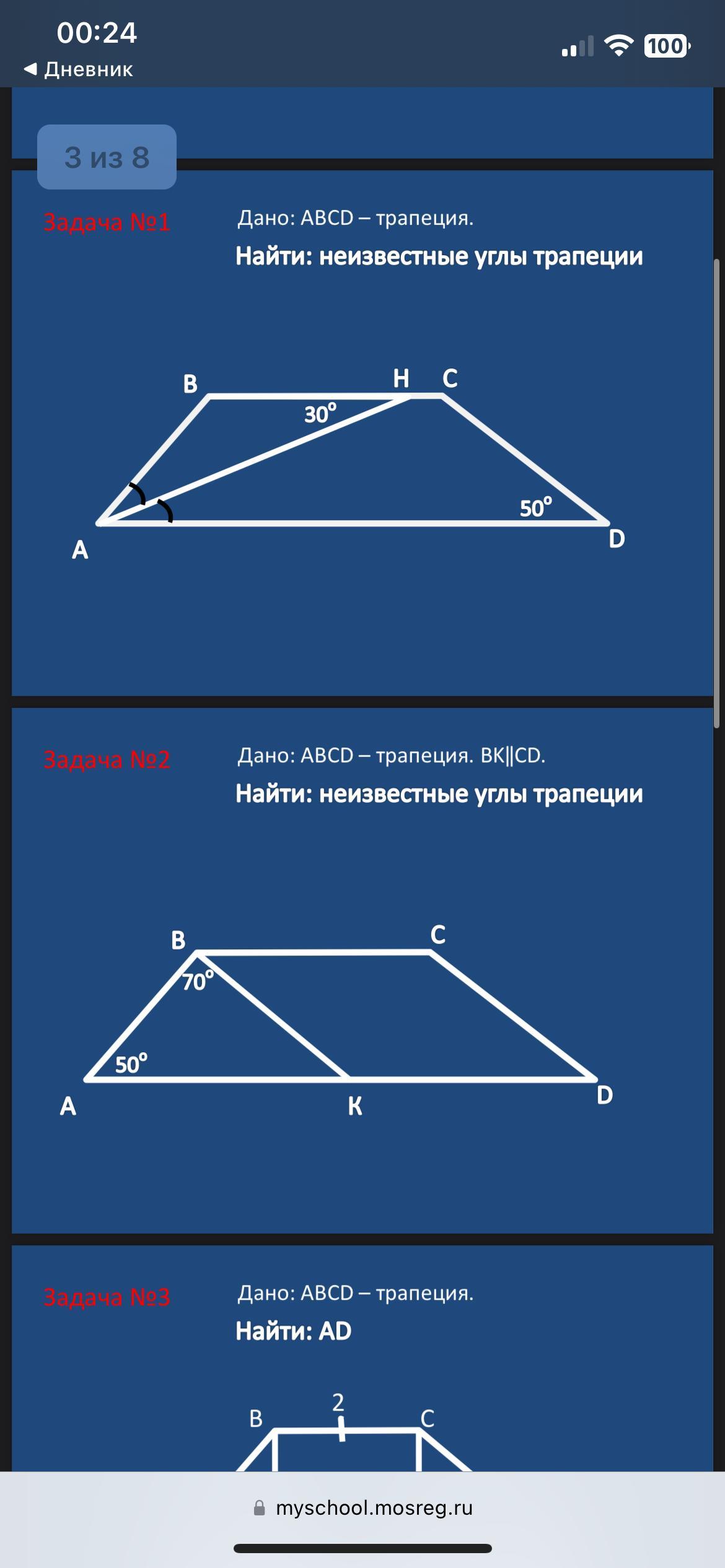
1) АВCD- трапеция , ВС || AD , ∠ACD = 50° ,
по условию АС - биссектриса ⇒ ∠BАН = ∠НAD
Но ∠НAD = ∠ВHА = 30° как внутренние накрест лежащие углы при
BC || AD и секущей АH .
Тогда и ∠BAH = 30°
∠BAD = ∠BAH + ∠HAD = 30° + 30° = 60°
Сумма углов трапеции , прилегающих к боковой стороне равна 180° ⇒ ∠BAD + ∠ABC = 180° ⇒ ∠ABC = 180° - 60° = 120° ,
∠ADC + ∠BCD = 180° ⇒ ∠BCD = 180° - ∠ADC = 180° - 50° = 130°