Предмет: Математика,
автор: zxzzxzxx
Двойной интеграл, помогите пожалуйста, очень подробно, если можете, с рисунком.
Приложения:
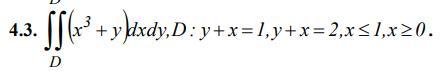
Ответы
Автор ответа:
1
Ответ:
Вычислить двойной интеграл по области D .
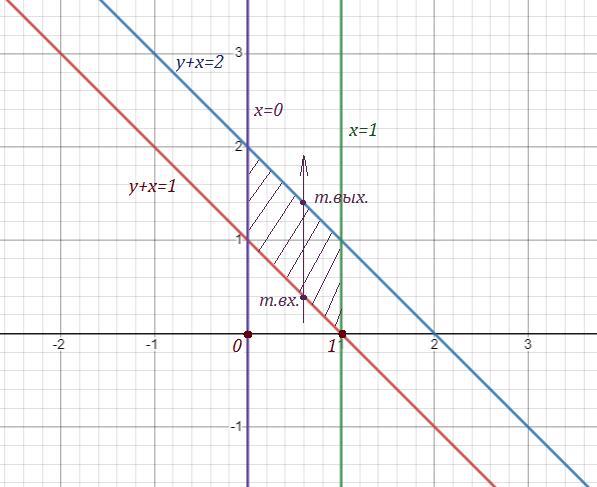
Область проектируется на ось ОХ в отрезок [ 0 ; 1 ] . Точка входа в область лежит на прямой у = 1 - х , точка выхода - на прямой у = 2 - х
Приложения:

NNNLLL54:
нажми "спасибо"
Похожие вопросы
Предмет: Математика,
автор: amezkakuromaku
Предмет: Алгебра,
автор: RBrobuxF
Предмет: История,
автор: eftfukui
Предмет: Математика,
автор: kardavaketino