sin (π:3-x:3)=1:2 розв'язати рівняння
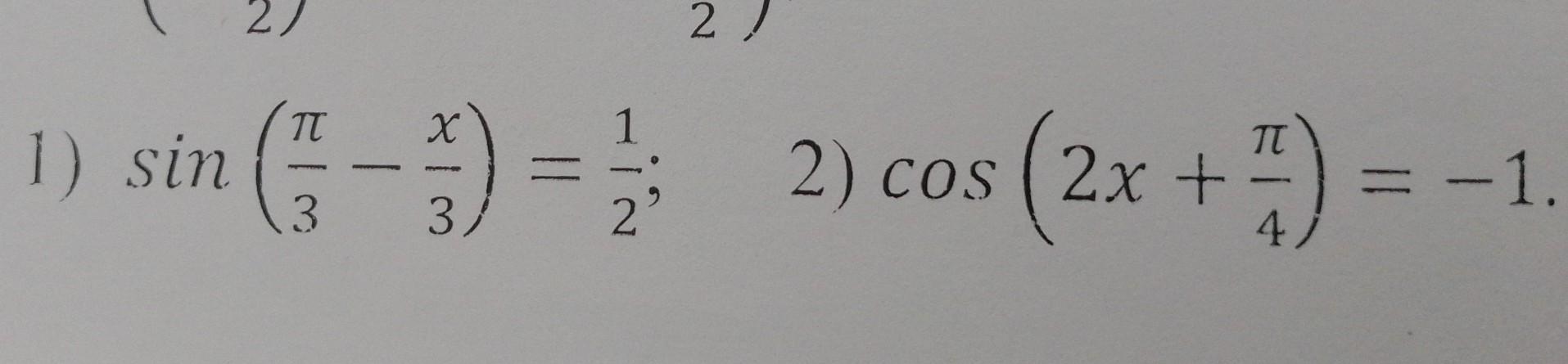
Ответы
Ответ:
Пошаговое объяснение:
Щоб розв'язати рівняння sin(π/3 - x/3) = 1/2, ми можемо скористатися властивостями тригонометричних функцій.
За формулою різниці для синуса, ми маємо:
sin(π/3 - x/3) = sin(π/3) * cos(x/3) - cos(π/3) * sin(x/3)
Знаючи, що sin(π/3) = √3/2 та cos(π/3) = 1/2, ми можемо підставити ці значення:
(√3/2) * cos(x/3) - (1/2) * sin(x/3) = 1/2
Помножимо обидві частини рівняння на 2, щоб позбутися від знаменника:
√3 * cos(x/3) - sin(x/3) = 1
Тепер ми можемо переписати рівняння у вигляді:
√3 * cos(x/3) = sin(x/3) + 1
За допомогою формули синуса подвійного кута, ми знаємо, що sin(2θ) = 2sin(θ) * cos(θ). Тому, ми можемо переписати рівняння як:
√3 * cos(x/3) = 2sin(x/3) * cos(x/3) + 1
Далі, зведемо подібні доданки:
√3 * cos(x/3) - 2sin(x/3) * cos(x/3) = 1
Факторизуємо ліву частину:
(cos(x/3)) * (√3 - 2sin(x/3)) = 1
Тепер, щоб розв'язати рівняння, ми розглянемо два випадки:
cos(x/3) = 1 і √3 - 2sin(x/3) = 1:
З першого рівняння отримуємо x/3 = 0, тобто x = 0.
Підставивши x = 0 у друге рівняння, отримуємо √3 - 0 = 1, що є правдою.
cos(x/3) ≠ 1 і √3 - 2sin(x/3) ≠ 1:
Ми можемо поділити обидві частини рівняння на (cos(x/3)) * (√3 - 2sin(x/3)), так як ми припускаємо, що цей вираз не дорівнює нулю:
1 = 1 / (cos(x/3)) * (√3 - 2sin(x/3))
Оскільки права частина рівняння дорівнює 1, це означає, що ліва частина також дорівнює 1.
Отже, випадок 2 не має розв'язків.
Таким чином, рівняння sin(π/3 - x/3) = 1/2 має єдиний розв'язок x = 0.