Question

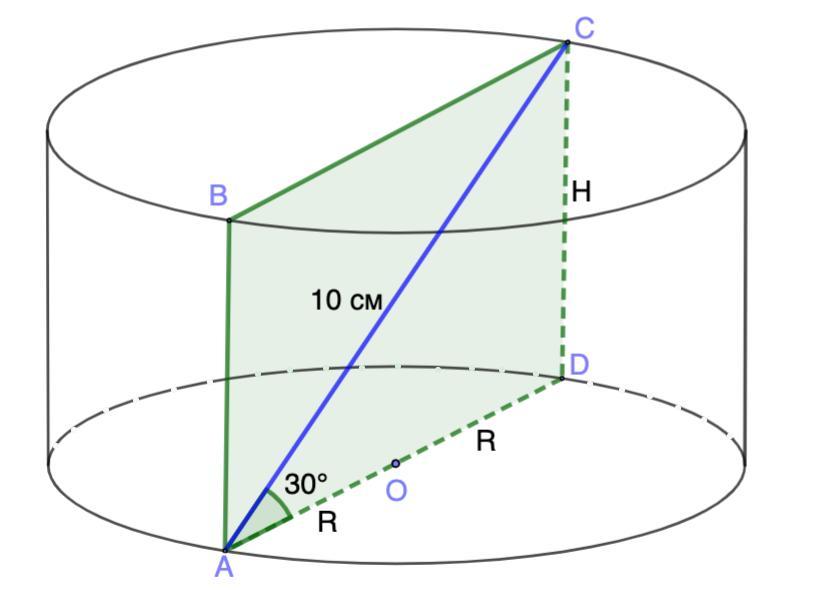
Прямокутник, діагональ якого дорівнює 10 см і нахилена до площини основи під кутом 30°, є осьовим перерізом циліндра. Знайдіть:
1) висоту циліндра;
2) радіус основи циліндра;
3) довжину кола основи циліндра.

Answer 1

Ответ:

1)   Высота цилиндра равна 5 см.

2)   Радиус основания цилиндра равен 5√3/2 см.

3)   Длина окружности основания цилиндра равна 5√3π см.

Объяснение:

Прямоугольник, диагональ которого равна 10 см и наклонена к плоскости основания под углом 30°, является осевым сечением цилиндра. Найти:

1) высоту цилиндра;

2) радиус основания цилиндра;

3) длину окружности основания цилиндра.

Дано: цилиндр;

ABCD - прямоугольник - осевое сечение;

АС = 10 см - диагональ;

∠CAD = 30°.

Найти: 1) высоту цилиндра;

2) радиус основания цилиндра;

3) длину окружности основания цилиндра.

Решение:

1)

Рассмотрим ΔACD - прямоугольный.

• Синус угла - отношение противолежащего катета к гипотенузе.

$\displaystyle sin\angle CAD=\frac{CD}{AC} \;\;\;\Rightarrow \;\;\;CD=sin\;30^0\cdot AC=\frac{1}{2}\cdot 10=5\;_{(CM)}$

Высота цилиндра равна 5 см.

2)

• Косинус угла - отношение прилежащего катета к гипотенузе.

$\displaystyle cos\angle CAD=\frac{AD}{AC} \;\;\;\Rightarrow \;\;\;AD=cos\;30^0\cdot AC=\frac{\sqrt{3} }{2}\cdot 10=5\sqrt{3} \;_{(CM)}$

AD - диаметр основания цилиндра.

• Радиус равен половине диаметра.

Радиус основания цилиндра равен 5√3/2 см.

3)

• Длину окружности основания цилиндра найдем по формуле:

                   с = πd,

где  d - диаметр цилиндра.

с = π · 5√3 = 5√3π (см)

Длина окружности основания цилиндра равна 5√3π см.

#SPJ1