Предмет: Алгебра,
автор: qggsgsywhahhs
розв'яжіть нерівність, у відповідь запишіть суму всіх цілих розв'язків, якщо нерівність має безліч цілих розв'язків, то запишіть у відповідь число 100
Приложения:
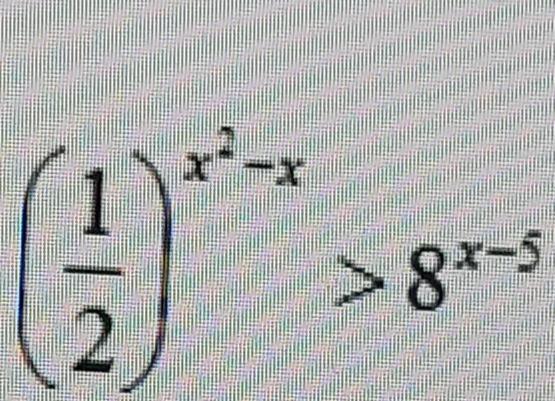
Ответы
Автор ответа:
1
Ответ:
-7
Объяснение:
1/2 = 2^(-1)
8 = 2^3
Следовательно, имеем
2^(-1*(x^2-x)) > 2^(3 * (x-5))
-1 * (x^2 - x) > 3 * (x-5)
x - x^2 > 3x - 15
-x^2 - 2x > -15
x^2 + 2x < 15
x^2 + 2x + 1 < 16
(x+1)^2 < 16
|x+1| < 4
-4-1 < x < 4-1
-5 < x < 3
Целые решения: -4, -3, -2, -1, 0, 1 и 2
Их сумма равна -4-3 = -7 (двойки еденицы и ноль сокращаются)
Похожие вопросы
Предмет: Литература,
автор: o8839001
Предмет: История,
автор: robert7877
Предмет: Математика,
автор: sekretalina28
Предмет: Алгебра,
автор: komka1994
Предмет: Математика,
автор: mehranhalafov484