Question

ДОПОМОЖІТЬ БУДЬ ЛАСКА ДУЖЕ-ДУЖЕ ПОТРІБНО ЗАЛИШИЛОСЯ МАЛО ЧАСУ!!!

Answer 1

Используем формулу косинуса угла между векторами.

cos α =(a*b)/(|a|*|b|).

Находим пары векторов, привязанных к вершинам треугольника.

AB = B(12; 2) – A(5; 6) = (7; -4), |AB| = √(7² + (-4)²) = √(49 + 16) = √65.

AC = C(5; 5) - A(5; 6) = (0; -1).   |AC| = √(0² + (-1)²) = √(0 + 6) = 1.

cos(A) = (7*0 + (-4)*(-1))/( √65*1) = (0 + 4)/√65 = 4/√65.

BA = -AB =  (-7; 4), |BA| = √(-7)² + 4²) = √(49 + 16) = √65.

BC = C(5; 5) - B(12; 2) = (-7; 3).   |AC| = √((-7)² + 3²) = √(49 + 9) = √58.

cos(B) = ((-7)*(-7) + 4*3)/( √65*√58) = (49 + 12)/√3770 = 61/√3770.

CA =  A(5; 6) - C(5; 5) = (0; 1), |CA| = √(0² + 1²) = √(0 + 1) = 1.

CB = -BC = (7; -3).   |CB| = √(7² + (-3)²) = √(49 + 9) = √58.

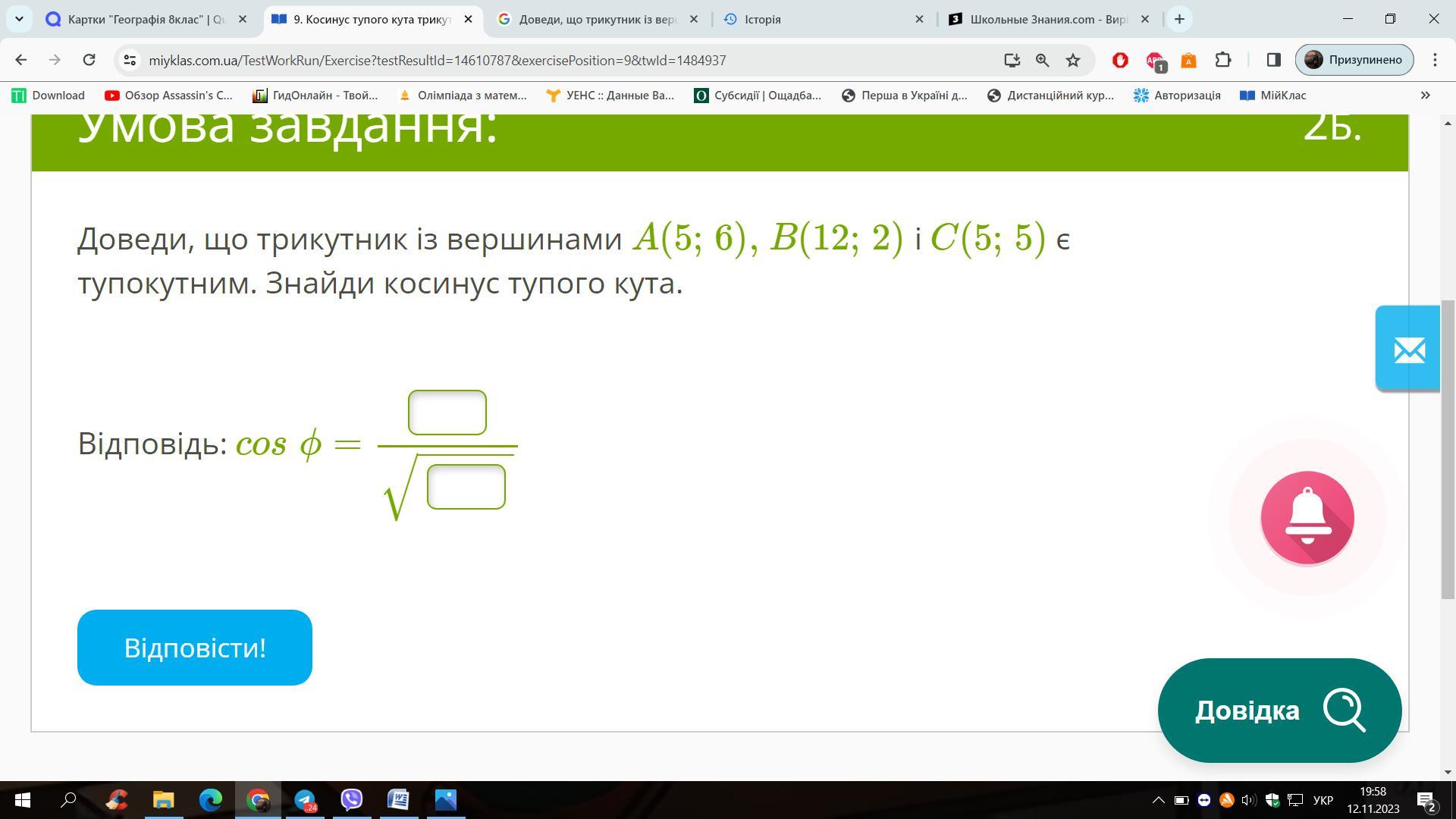
cos(C) = (0*7 + 1*(-3))/( 1*√58) = (0 - 3)/√58 = -3/√58.

Как видим, косинус угла С имеет отрицательное значение, поэтому угол С тупой, а треугольник АВС – тупоугольный, что и требовалось доказать.