Предмет: Алгебра,
автор: accountzablokirovan
АЛГЕБРА! Только 1 и 3. СРОЧНО!
ЗАДАНИЕ : Знайдіть множину розв'язків системи нерівностей
Приложения:
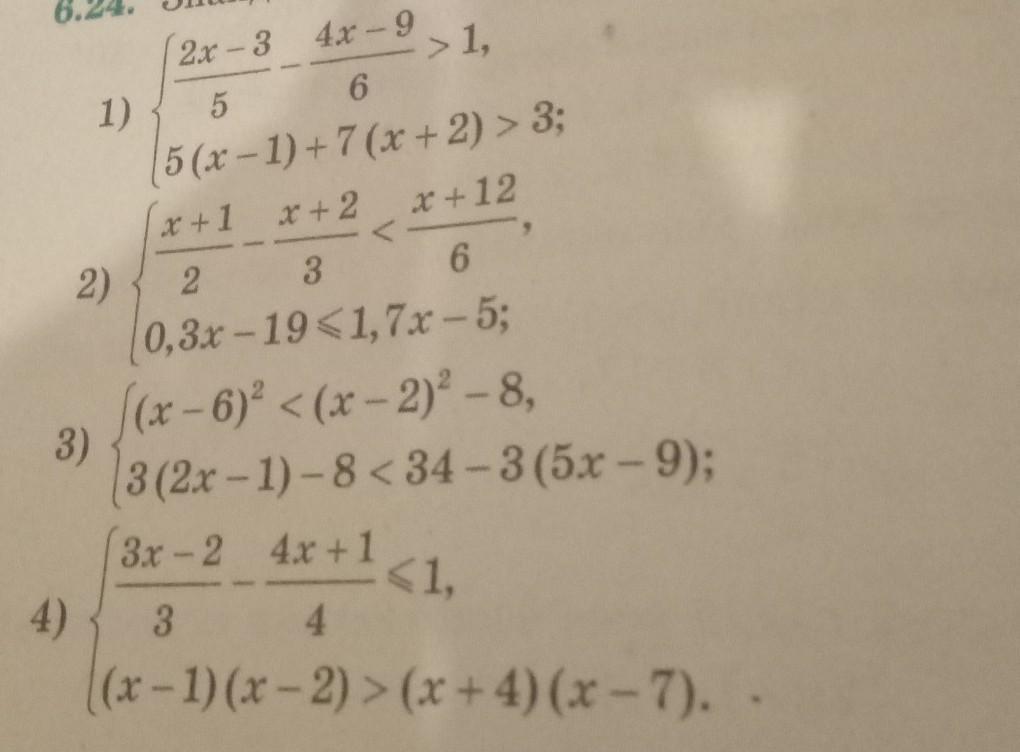
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: aldiarbekseiit
Предмет: Русский язык,
автор: mrqsay2
Предмет: Английский язык,
автор: alloa6688
Предмет: Литература,
автор: karagulovaajgerim89
Предмет: Русский язык,
автор: koslovdana