Предмет: Математика,
автор: ffh558129
Определить то значение параметра
A, при котором f (x) будет непрерывной (если это возможно). Сделать рисунок.
Расписано
Приложения:
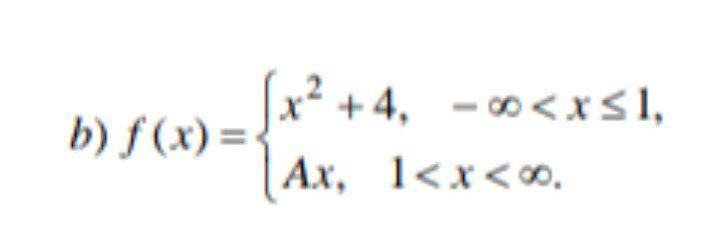
Ответы
Автор ответа:
1
Ответ:
A=5
Пошаговое объяснение:
- Чтобы функция у = f(х), определенная в некоторой окрестности точки x₀, была непрерывна в точке x₀, необходимо и достаточно, чтобы существовали равные односторонние пределы и они были бы равны значению функции в точке х₀:
- f(х₀-0)=f(х₀+0)=f(х₀).
Значит, нам нужно путем доопределения функции f(x) = Ax через параметр А, получить
при этом
f(1) = 5
Таким образом, при А=5 функция будет непрерывна в точке х₀ = 1
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: sayrex001
Предмет: Химия,
автор: nataaleks1974z
Предмет: Математика,
автор: aylinmukhamadieva15
Предмет: Алгебра,
автор: uktinq
Предмет: Другие предметы,
автор: sologubovaola9