Предмет: Алгебра,
автор: iskanderovsamir4
пожалуйста помогите с контрольной умоляю даю 40 балов
Приложения:

Ответы
Автор ответа:
0
Ответ:
Объяснение:
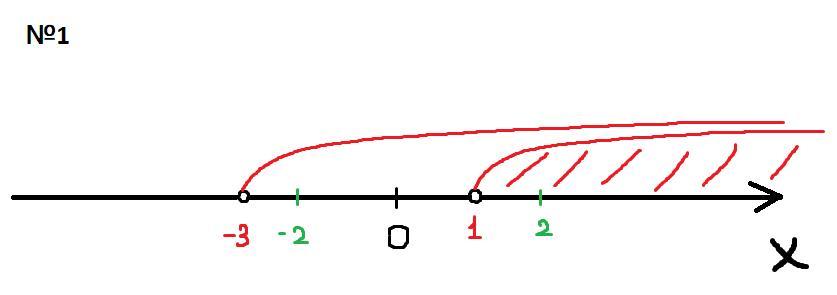
№1
Ответ: 2
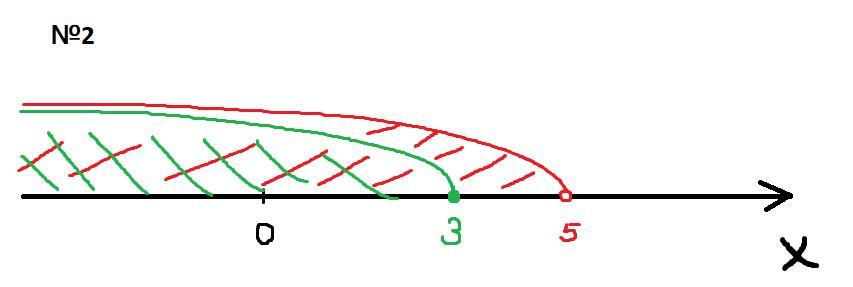
№2
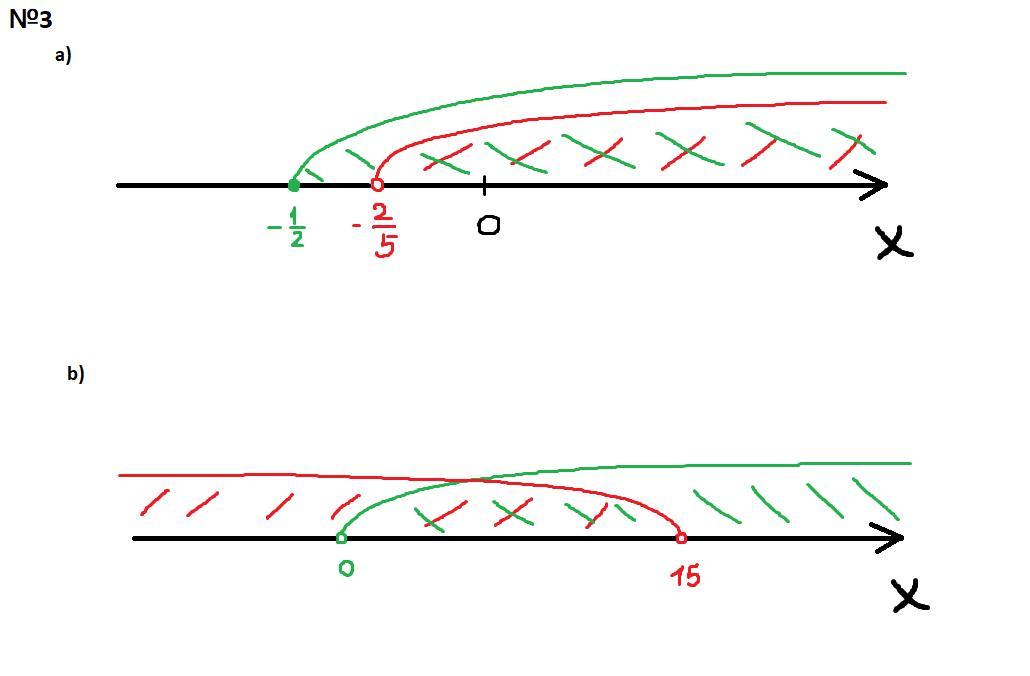
№3
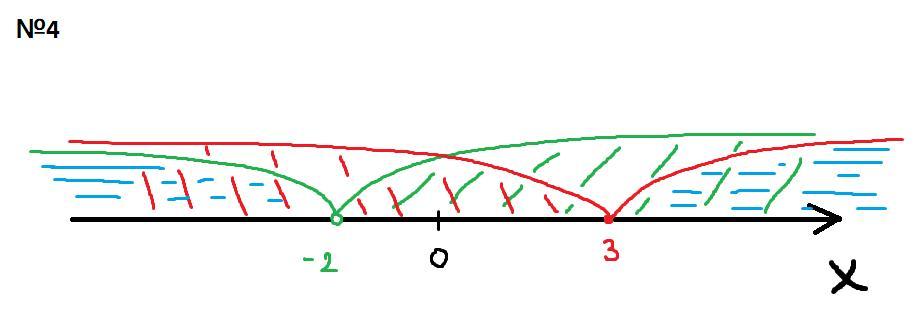
№4
==================================
ОДЗ:
==================================
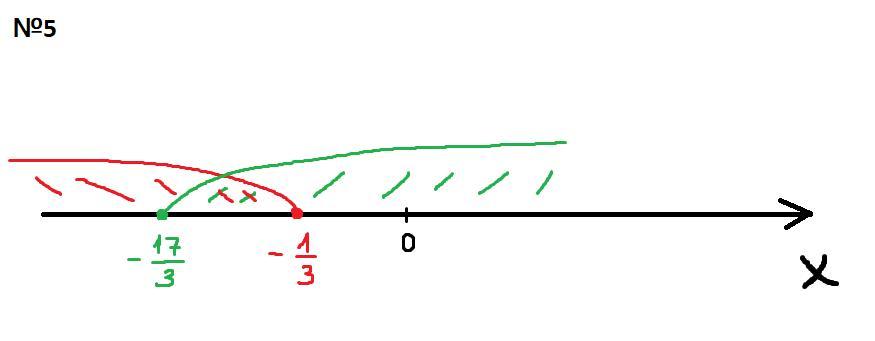
№5
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Химия,
автор: aiymalikyzy11
Предмет: Математика,
автор: mtsoy509
Предмет: Английский язык,
автор: moneylonger