Установіть відповідність між функціями та їхніми графіками.функції:1)у=-х²+1:2)у=ײ-2:3)3(×+3)²:4)у=(×+2)²+2:5)у=-2(×-1)²+3.
Ответы
Відповідь:
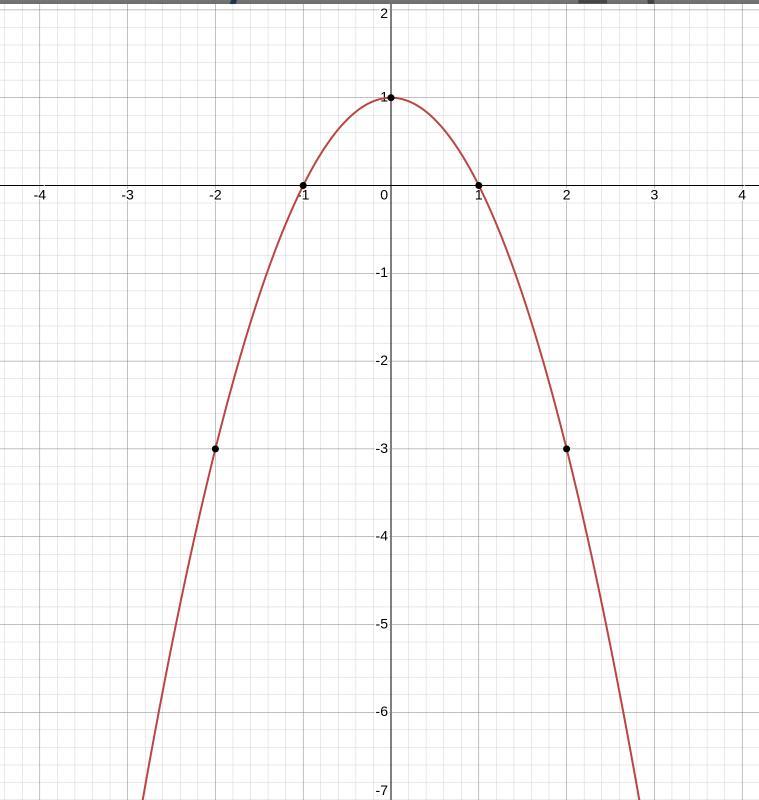
1) Парабола піднята на 1 одиницю в гору із вітками нахиленими вниз
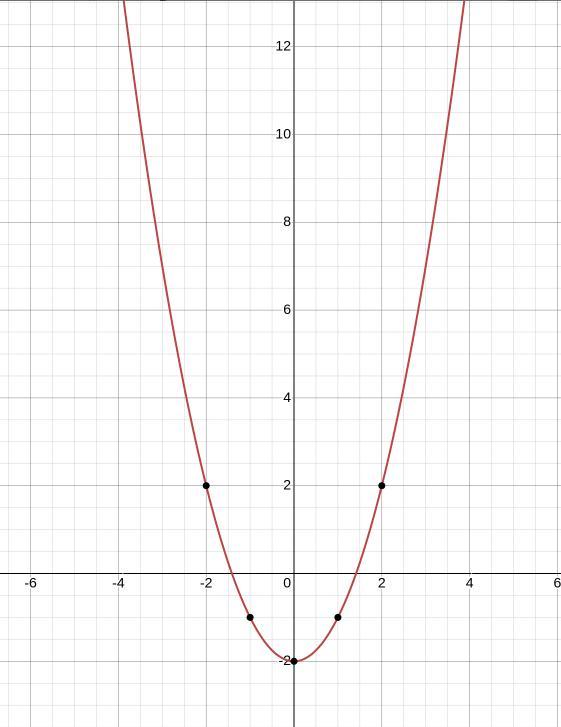
2) Парабола опущена на 2 одиниці вниз із вітками напрямленими вгору
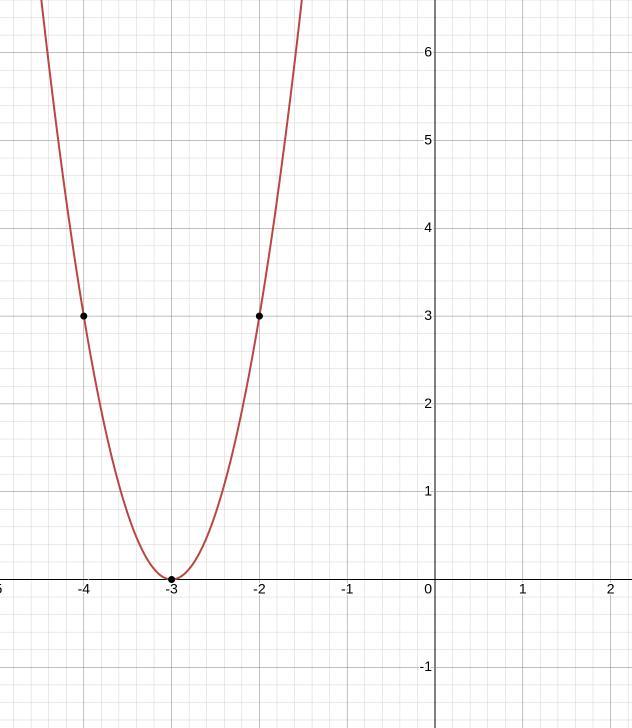
3) Парабола із одним нулем, який є вершиною в точці (-3;0), із вітками, нахиленими вгору
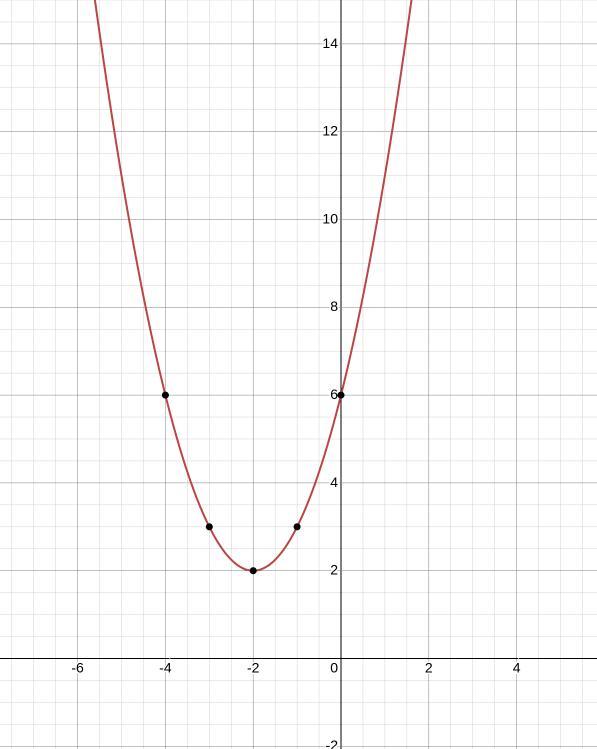
4) Парабола, яка не доторкається до осі іксів, із вершиною в точці (-2;2), із вітками напрямленими вгору
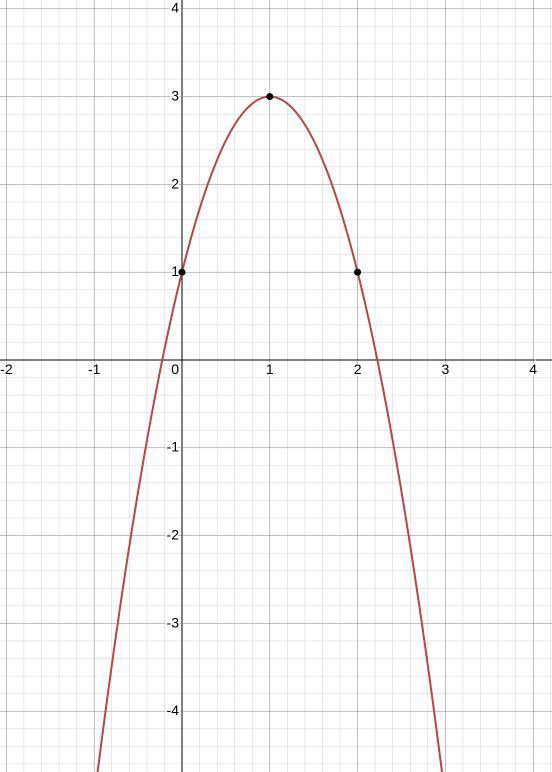
5)Парабола із вершиною в точці (1;3), вітками напрямлена вниз, із нулями в точках і
В поясненні прикріплені самі графіки. Всі формули я брав із НМТ
Пояснення:
1)
Дивимось уважно: - це парабола вітками вгору. А в нашої функції при іксу стоїть "-", одже це буде парабола вітками вниз, а "+1" означає, що вона буде піднята на 1 одиницю в гору.
2) - ця ситуація схожа до попередньої, тільки тут ікс додатній, одже парабола буде вітками вгору, а "-2" означає, що вона опущена на 2 одиниці вниз.
3) давайте спочатку розкриємо дужки:
Одже функція виглядає так:
. Як правило щоб знайти графік такої функції параболи потрібно спочатку знайти вершину, потім її нулі, і зєднати все:
1. Знаходимо вершину () (формулу я взяв із формул НМТ, і прикріпив її зображення у відповіді)
. Тепер підставляємо наше
в функцію і отримаємо
.
. Як бачимо шукаючи вершину ми знайши єдиний нуль, як за сумісництвом є вершиною. Оскільки коефіцієнт a - додатній парабола напрямлена вітками вгору. Із вершиною в точці (-3; 0)
4) Тут будемо робити все як в попередньому випадку: розкриваємо дужки:
. Графік виглядає так:
. Шукаємо нулі, а потім вершину:
1. .
Дискримінант вийшов відємний, тому парабола - немає нулів. Шукаємо вершину():
2.
Коефіцієнт а - додатній (він дорівнює 1), тому парабола напрямлена вітками в гору, із вершини в точці (-2;2)
5)
Тобто:
1. Знаходимо нулі параболи:
2. Знаходимо вершину параболи:
Одже графік функції - парабола із вершиною в точці (1;3) та нулями і