Фаст дайс много балов
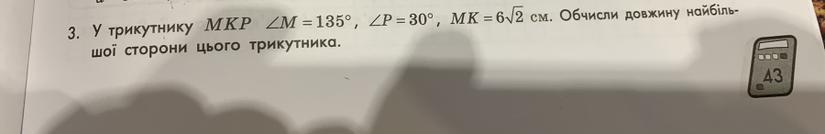
Ответы
Оригінальна аватарка
Для вирішення цієї задачі ми використовуємо закон синусів.
У нашому випадку, ми знаємо, що ∠ZM = 135°, ∠P = 30° і MK = 6√2 см.
Ми можемо обчислити ∠K, третій кут трикутника, віднявши від 180° суму двох інших кутів:
∠K = 180° - 135° - 30° = 15°
Тепер ми можемо використати закон синусів, щоб знайти довжину сторони ZK. Закон синусів в цьому випадку виглядає так:
ZK / sin(∠K) = MK / sin(∠ZM)
Ми можемо переставити це рівняння, щоб знайти ZK:
ZK = MK * sin(∠K) / sin(∠ZM)
Підставляючи відомі значення, ми отримуємо:
ZK = 6√2 см * sin(15°) / sin(135°)
Обчислюючи це, ми отримуємо довжину сторони ZK.
Ми знаємо, що sin(15°) приблизно дорівнює 0.2588, а sin(135°) дорівнює √2/2 або приблизно 0.7071.
Тоді ми отримуємо:
ZK = 6√2 см * 0.2588 / 0.7071
Обчислюючи це, ми отримуємо:
ZK ≈ 2.2 см
Отже, найбільша сторона трикутника MKP має довжину приблизно 2.2 см.