Question

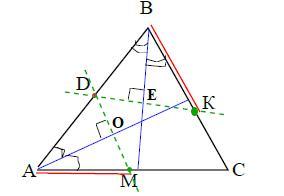
Через середину D сторони AB трикутника ABC прове-
дено прямі, перпендикулярні до бісектрис кутів ABC

і BAC. Ці прямі перетинають сторони AC і BC у точ-
ках M і K відповідно. Доведіть, що АМ = ВK.
ДАЮ 50 балов

Answer 1

Ответ:

Объяснение:

Дано:
AD = DB
АК - биссектриса ∠ВАС
ВМ - биссектриса ∠АВС
DM⊥АК  
DK⊥BM
_________

Док., AM = BK

1) Рассмотрим ΔADM и ΔDBK.
   Т.к. DM⊥АК по условию, то АО является одновременно и биссектрисой (по условию; ∠ВАО = ∠ОАМ) и высотой. Следовательно,
ΔADM - равнобедренный и AD = AM.

Аналогично, ВЕ является и биссектрисой и высотой, значит, и
ΔADM - равнобедренный, DB = BK.

2) Но AD = DB по условию, следовательно, и
   АM = ВК, ч.т.д.